What is Concurrent Programming?

TL;DR

We have defined concurrent programming informally, based upon your experience with computer systems. Our goal is to study concurrency abstractly, rather than a particular implementation in a specific programming language or operating system. We have to carefully specify the abstraction that describe the allowable data structures and operations. In the next chapter, we will define the concurrent programming abstraction and justify its relevance. We will also survey languages and systems that can be used to write concurrent programs.

Introduction

An ordinary program consists of data declarations and assignment and control-flow statements in a programming language. Modern languages include structures such as procedures and modules for organizing large software systems through abstraction and encapsulation, but the statements that are actually executed are still the elementary statements that compute expressions, move data and change the flow of control. In fact, these are precisely the instructions that appear in the machine code that results from compilation. These machine instructions are executed sequentially on a computer and access data stored in the main or secondary memories.

A concurrent program is a set of sequential programs that can be executed in parallel. We use the word process for the sequential programs that comprise a concurrent program and save the term program for this set of processes.

Traditionally, the word parallel is used for systems in which the executions of several programs overlap in time by running them on separate processors. The word concurrent is reserved for potential parallelism, in which the executions may, but need not, overlap; instead, the parallelism may only be apparent since it may be implemented by sharing the resources of a small number of processors, often only one. Concurrency is an extremely useful abstraction because we can better understand such a program by pretending that all processes are being executed in parallel. Conversely, even if the processes of a concurrent program are actually executed in parallel on several processors, understanding its behavior is greatly facilitated if we impose an order on the instructions that is compatible with shared execution on a single processor. Like any abstraction, concurrent programming is important because the behavior of a wide range of real systems can be modeled and studied without unnecessary detail.

In this book we will define formal models of concurrent programs and study algorithms written in these formalisms. Because the processes that comprise a concurrent program may interact, it is exceedingly difficult to write a correct program for even the simplest problem. New tools are needed to specify, program and verify these programs. Unless these are understood, a programmer used to writing and testing sequential programs will be totally mystified by the bizarre behavior that a concurrent program can exhibit.

Concurrent programming arose from problems encountered in creating real systems. To motivate the concurrency abstraction, we present a series of examples of real-world concurrency.

Concurrency as abstract parallelism

It is difficult to intuitively grasp the speed of electronic devices. The fingers of a fast typist seem to fly across the keyboard, to say nothing of the impression of speed given by a printer that is capable of producing a page with thousands of characters every few seconds. Yet these rates are extremely slow compared to the time required by a computer to process each character.

As I write, the clock speed of the central processing unit (CPU) of a personal computer is of the order of magnitude of one gigahertz (one billion times a second). That is, every nanosecond (one-billionth of a second), the hardware clock ticks and the circuitry of the CPU performs some operation. Let us roughly estimate that it takes ten clock ticks to execute one machine language instruction, and ten instructions to process a character, so the computer can process the character you typed in one hundred nanoseconds, that is 0.0000001 of a second:

To get an intuitive idea of how much effort is required on the part of the CPU, let us pretend that we are processing the character by hand. Clearly, we do not consciously perform operations on the scale of nanoseconds, so we will multiply the time scale by one billion so that every clock tick becomes a second:

Thus we need to perform 100 seconds of work out of every billion seconds. How much is a billion seconds? Since there are 60 x 60 x 24 = 86,400 seconds in a day, a billion seconds is 1,000,000,000/86,400 = 11,574 days or about 32 years. You would have to invest 100 seconds every 32 years to process a character, and a 3,000-character page would require only (3,000 x 100)/(60 x 60) ~ 83 hours over half a lifetime. This is hardly a strenuous job!

The tremendous gap between the speeds of human and mechanical processing on the one hand and the speed of electronic devices on the other led to the develop- ment of operating systems which allow I/O operations to proceed “in parallel” with computation. On a single CPU, like the one in a personal computer, the processing required for each character typed on a keyboard cannot really be done in parallel with another computation, but it is possible to “steal” from the other computation the fraction of a microsecond needed to process the character. As can be seen from the numbers in the previous paragraph, the degradation in performance will not be noticeable, even when the overhead of switching between the two computations is included.

What is the connection between concurrency and operating systems that overlap I/O with other computations? It would theoretically be possible for every program to include code that would periodically sample the keyboard and the printer to see if they need to be serviced, but this would be an intolerable burden on programmers by forcing them to be fully conversant with the details of the operating system. In- stead, I/O devices are designed to interrupt the CPU, causing it to jump to the code to process a character. Although the processing is sequential, it is conceptually simpler to work with an abstraction in which the I/O processing performed as the result of the interrupt is a separate process, executed concurrently with a process doing another computation. The following diagram shows the assignment of the CPU to the two processes for computation and I/O.

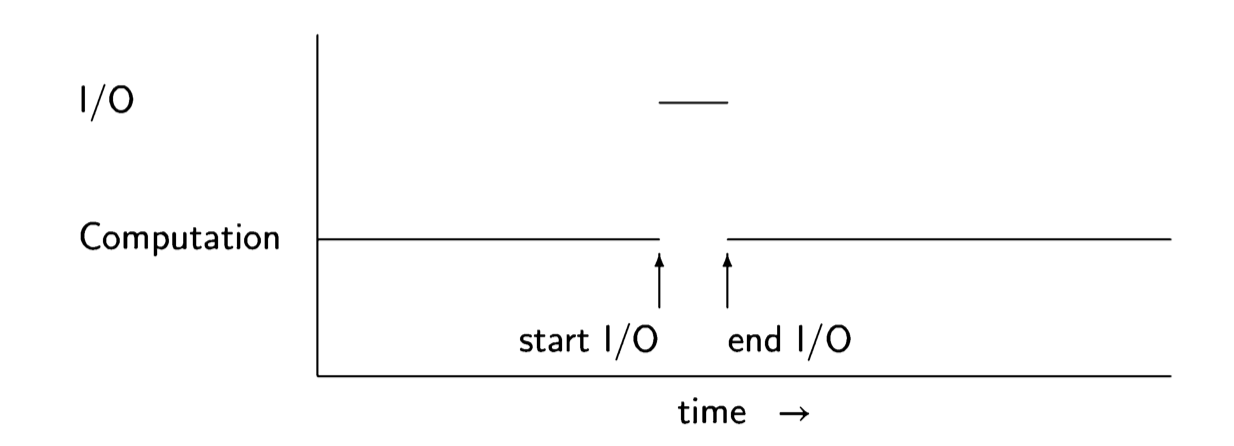
Multitasking

Multitasking is a simple generalization from the concept of overlapping I/O with a computation to overlapping the computation of one program with that of another. Multitasking is the central function of the kernel of all modern operating systems. A scheduler program is run by the operating system to determine which process should be allowed to run for the next interval of time. The scheduler can take into account priority considerations, and usually implements time-slicing, where com- putations are periodically interrupted to allow a fair sharing of the computational resources, in particular, of the CPU. You are intimately familiar with multitask- ing; it enables you to write a document on a word processor while printing another document and simultaneously downloading a file.

Multitasking has become so useful that modern programming languages support it within programs by providing constructs for multithreading. Threads enable the programmer to write concurrent (conceptually parallel) computations within a single program. For example, interactive programs contain a separate thread for handling events associated with the user interface that is run concurrently with the main thread of the computation. It is multithreading that enables you to move the mouse cursor while a program is performing a computation.

Multiple computers

The days of one large computer serving an entire organization are long gone. To- day, computers hide in unforeseen places like automobiles and cameras. In fact, your personal “computer” (in the singular) contains more than one processor: the graphics processor is a computer specialized for the task of taking information from the computer’s memory and rendering it on the display screen. I/O and commu- nications interfaces are also likely to have their own specialized processors. Thus, in addition to the multitasking performed by the operating systems kernel, parallel processing is being carried out by these specialized processors.

The use of multiple computers is also essential when the computational task re- quires more processing than is possible on one computer. Perhaps you have seen pictures of the “server farms” containing tens or hundreds of computers that are used by Internet companies to provide service to millions of customers. In fact, the entire Internet can be considered to be one distributed system working to dissemi- nate information in the form of email and web pages.

Somewhat less familiar than distributed systems are multiprocessors, which are systems designed to bring the computing power of several processors to work in concert on a single computationally-intensive problem. Multiprocessors are exten- sively used in scientific and engineering simulation, for example, in simulating the atmosphere for weather forecasting and studying climate.

The challenge of concurrent programming

The challenge in concurrent programming comes from the need to synchronize the execution of different processes and to enable them to communicate. If the processes were totally independent, the implementation of concurrency would only require a simple scheduler to allocate resources among them. But if an I/O process accepts a character typed on a keyboard, it must somehow communicate it to the process running the word processor, and if there are multiple windows on a display, processes must somehow synchronize access to the display so that images are sent to the window with the current focus.

It turns out to be extremely difficult to implement safe and efficient synchronization and communication. When your personal computer freezes up or when using one application causes another application to crash, the cause is generally an error in synchronization or communication. Since such problems are time and situation dependent, they are difficult to reproduce, diagnose and correct.

The aim of this book is to introduce you to the constructs, algorithms and systems that are used to obtain correct behavior of concurrent and distributed programs. The choice of construct, algorithm or system depends critically on assumptions concerning the requirements of the software being developed and the architecture of the system that will be used to execute it. This book presents a survey of the main ideas that have been proposed over the years; we hope that it will enable you to analyze, evaluate and employ specific tools that you will encounter in the future.

Transition

The Concurrent Programming Abstraction

TL;DR

This chapter has presented and justified the concurrent program abstraction as the interleaved execution of atomic statements. The specification of atomic statements is a basic task in the definition of a concurrent system; they can be machine instructions or higher-order statements that are executed atomically. We have also shown how concurrent programs can be written and executed using a concurrency simulator (Pascal and C in BACD, a programming language (Ada and Java) or simulated with a model checker (Promela in Spin). But we have not actually solved any problems in concurrent programming. The next three chapters will focus on the critical section problem, which is the most basic and important problem to be solved in concurrent programming.

The role of abstraction

Scientific descriptions of the world are based on abstractions. A living animal is a system constructed of organs, bones and so on. These organs are composed of cells, which in turn are composed of molecules, which in turn are composed of atoms, which in turn are composed of elementary particles. Scientists find it convenient (and in fact necessary) to limit their investigations to one level, or maybe two levels, and to abstract away from lower levels. Thus your physician will listen to your heart or look into your eyes, but he will not generally think about the molecules from which they are composed. There are other specialists, pharmacologists and biochemists, who study that level of abstraction, in turn abstracting away from the quantum theory that describes the structure and behavior of the molecules.

In computer science, abstractions are just as important. Software engineers gener- ally deal with at most three levels of abstraction:

Systems and libraries Operating systems and libraries—often called Application Program Interfaces (API)—define computational resources that are available to the programmer. You can open a file or send a message by invoking the proper procedure or function call, without knowing how the resource is im- plemented.

Programming languages A programming language enables you to employ the computational power of a computer, while abstracting away from the details of specific architectures.

Instruction sets Most computer manufacturers design and build families of CPUs which execute the same instruction set as seen by the assembly language programmer or compiler writer. The members of a family may be implemented in totally different ways—emulating some instructions in software or using memory for registers—but a programmer can write a compiler for that instruction set without knowing the details of the implementation.

Of course, the list of abstractions can be continued to include logic gates and their implementation by semiconductors, but software engineers rarely, if ever, need to work at those levels. Certainly, you would never describe the semantics of an assignment statement like $x\leftarrow y+z$ in terms of the behavior of the electrons within the chip implementing the instruction set into which the statement was compiled.

Two of the most important tools for software abstraction are encapsulation and concurrency.

Encapsulation achieves abstraction by dividing a software module into a public specification and a hidden implementation. The specification describes the available operations on a data structure or real-world model. The detailed implementation of the structure or model is written within a separate module that is not accessible from the outside. Thus changes in the internal data representation and algorithm can be made without affecting the programming of the rest of the system. Modern programming languages directly support encapsulation.

Concurrency is an abstraction that is designed to make it possible to reason about the dynamic behavior of programs. This abstraction will be carefully explained in the rest of this chapter. First we will define the abstraction and then show how to relate it to various computer architectures. For readers who are familiar with machine-language programming, Sections 2.8—2.9 relate the abstraction to machine instructions; the conclusion is that there are no important concepts of concurrency that cannot be explained at the higher level of abstraction, so these sections can be skipped if desired. The chapter concludes with an introduction to concurrent programming in various languages and a supplemental section on a puzzle that may help you understand the concept of state and state diagram.

Concurrent execution as interleaving of atomic statements

We now define the concurrent programming abstraction that we will study in this textbook. The abstraction is based upon the concept of a (sequential) process, which we will not formally define. Consider it as a normal program fragment written in a programming language. You will not be misled if you think of a process as a fancy name for a procedure or method in an ordinary programming language.

Definition 2.1 A concurrent program consists of a finite set of (sequential) pro- cesses. The processes are written using a finite set of atomic statements. The execution of a concurrent program proceeds by executing a sequence of the atomic statements obtained by arbitrarily interleaving the atomic statements from the pro- cesses. A computation is an execution sequence that can occur as a result of the interleaving. Computations are also called scenarios.

Definition 2.2 During a computation the control pointer of a process indicates the next statement that can be executed by that process. Each process has its own control pointer.

Computations are created by interleaving, which merges several statement streams. At each step during the execution of the current program, the next statement to be executed will be chosen from the statements pointed to by the control pointers cp of the processes.

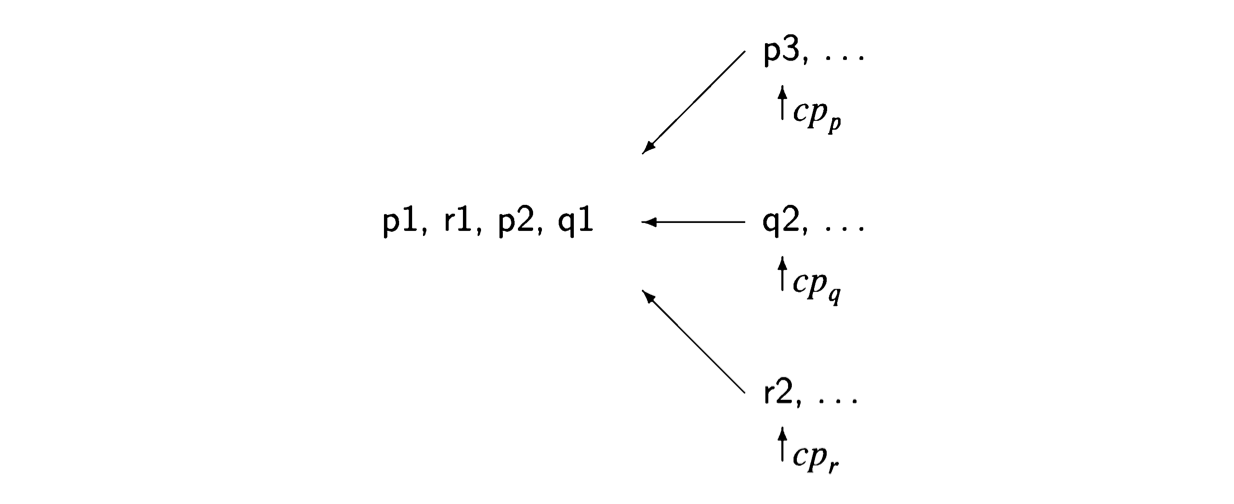
Suppose that we have two processes, p composed of statements $p1$ followed by $p2$ and $q$ composed of statements $q1$ followed by $q2$, and that the execution is started with the control pointers of the two processes pointing to $p1$ and $q1$. Assuming that the statements are assignment statements that do not transfer control, the possible scenarios are:

\[ p1 \rightarrow q1 \rightarrow p2 \rightarrow q2, \] \[ p1 \rightarrow q1 \rightarrow q2 \rightarrow p2, \] \[ p1 \rightarrow p2 \rightarrow q1 \rightarrow q2, \] \[ q1 \rightarrow p1 \rightarrow q2 \rightarrow p2, \] \[ q1 \rightarrow p1 \rightarrow p2 \rightarrow q2, \] \[ q1 \rightarrow q2 \rightarrow p1 \rightarrow p2. \]

Note that $p2 \rightarrow p1 \rightarrow q1 \rightarrow q2 $ is not a scenario, because we respect the sequential execution of each individual process, so that $p2$ cannot be executed before $p1$.

We will present concurrent programs in a language-independent form, because the concepts are universal, whether they are implemented as operating systems calls, directly in programming languages like Ada or Java, or in a model specification language like Promela. The notation is demonstrated by the following trivial two- process concurrent algorithm:

Algorithm 2.1

The program is given a title, followed by declarations of global variables, followed by two columns, one for each of the two processes, which by convention are named process p and process q. Each process may have declarations of local variables, followed by the statements of the process. We use the following convention:

States

The execution of a concurrent program is defined by states and transitions between states. Let us first look at these concepts in a sequential version of the above algorithm:

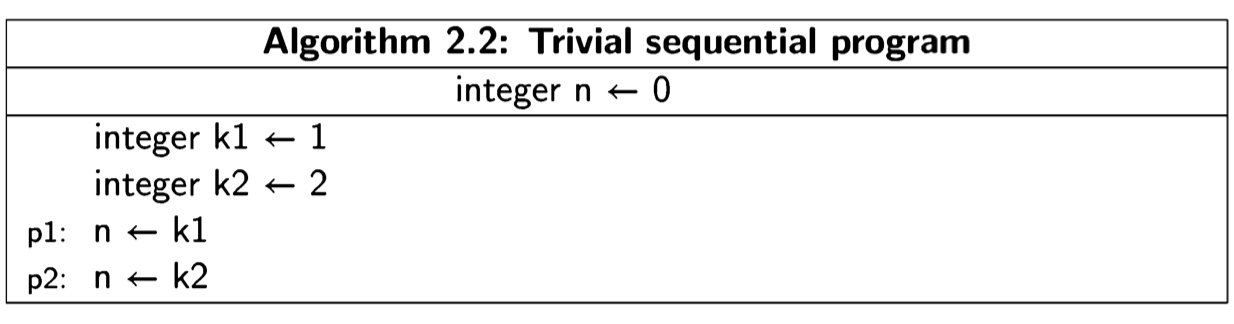
Algorithm 2.2

At any time during the execution of this program, it must be in a state defined by the value of the control pointer and the values of the three variables. Executing a statement corresponds to making a transition from one state to another. It is clear that this program can be in one of three states: an initial state and two other states obtained by executing the two statements. This is shown in the following diagram, where a node represents a state, arrows represent the transitions, and the initial state is pointed to by the short arrow on the left:

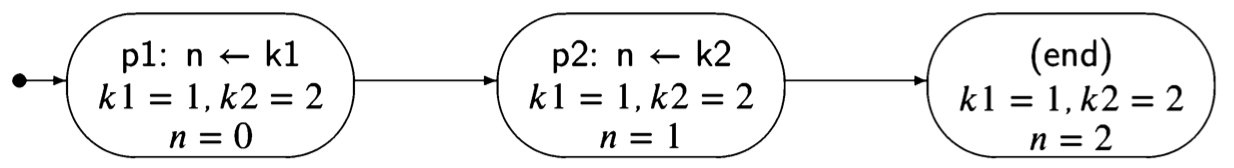
Consider now the trivial concurrent program Algorithm 2.1 There are two pro- cesses, so the state must include the control pointers of both processes. Further- more, in the initial state there is a choice as to which statement to execute, so there are two transitions from the initial state.

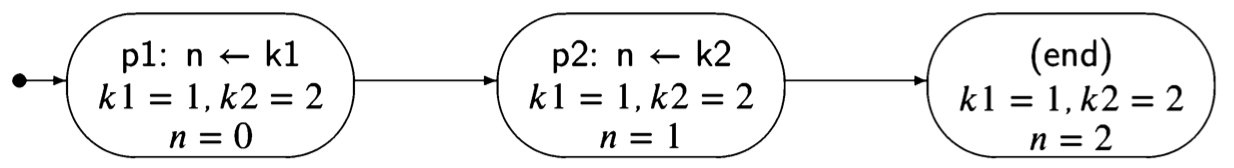
The lefthand states correspond to executing p1 followed by q1, while the righthand states correspond to executing q1 followed by pl. Note that the computation can terminate in two different states (with different values of 1), depending on the interleaving of the statements.

Definition 2.3 The state of a (concurrent) algorithm is a tuple consisting of one element for each process that is a label from that process, and one element for each global or local variable that is a value whose type is the same as the type of the variable.

The number of possible states—the number of tuples—is quite large, but in an execution of a program, not all possible states can occur. For example, since no values are assigned to the variables k1 and k2 in Algorithm 2.1, no state can occur in which these variables have values that are different from their initial values.

Definition 2.4 Let $s_1$ and $s_2$ be states. There is a transition between $s_1$, and $s_2$ if executing a statement in state $s_1$ changes the state to $s_2$. The statement executed must be one of those pointed to by a control pointer in $s_1$.

Definition 2.5 A state diagram is a graph defined inductively. The initial state diagram contains a single node labeled with the initial state. If state $s_1$ labels a node in the state diagram, and if there is a transition from $s_1$ to $s_2$, then there is a node labeled $s_2$ in the state diagram and a directed edge from $s_1$ to $s_2$.

For each state, there is only one node labeled with that state.

The set of reachable states is the set of states in a state diagram.

It follows from the definitions that a computation (scenario) of a concurrent pro- gram is represented by a directed path through the state diagram starting from the initial state, and that all computations can be so represented. Cycles in the state diagram represent the possibility of infinite computations in a finite graph.

The state diagram for Algorithm 2.1 shows that there are two different scenarios, each of which contains three of the five reachable states.

Scenarios

A scenario is defined by a sequence of states. Since diagrams can be hard to draw, especially for large programs, it is convenient to use a tabular representation of scenarios. This is done simply by listing the sequence of states in a table; the columns for the control pointers are labeled with the processes and the columns for the variable values with the variable names. The following table shows the scenario of Algorithm 2.1 corresponding to the lefthand path:

In a state, there may be more than one statement that can be executed. We use bold font to denote the statement that was executed to get to the state in the following row.

Rows represent states. If the statement executed is an assignment statement, the new value that is assigned to the variable is a component of the next state in the scenario, which is found in the next row.

Justification of the abstraction

Clearly, it doesn’t make sense to talk of the global state of a computer system, or of coordination between computers at the level of individual instructions. The electrical signals in a computer travel at the speed of light, about $ 2·10^8 \frac{m}{sec}$, and the clock cycles of modern CPUs are at least one gigahertz, so information cannot travel more than $ 2x10^8· 10^{-9} = 0.2 m$ during a clock cycle of a CPU. There is simply not enough time to coordinate individual instructions of more than one CPU.

Nevertheless, that is precisely the abstraction that we will use! We will assume that we have a bird’s-eye view of the global state of the system, and that a state- ment of one process executes by itself and to completion, before the execution of a statement of another process commences.

It is a convenient fiction to regard the execution of a concurrent program as being carried out by a global entity who at each step selects the process from which the next statement will be executed. The term interleaving comes from this image: just as you might interleave the cards from several decks of playing cards by selecting cards one by one from the decks, so we regard this entity as interleaving statements by selecting them one by one from the processes. The interleaving is arbitrary, that is—with one exception to be discussed in Section 2.7—we do not restrict the choice of the process from which the next statement is taken.

The abstraction defined is highly artificial, so we will spend some time justifying it for various possible computer architectures.

Multitasking systems

Consider the case of a concurrent program that is being executed by multitasking, that is, by sharing the resources of one computer. Obviously, with a single CPU there is no question of the simultaneous execution of several instructions. The se- lection of the next instruction to execute is carried out by the CPU and the operating system. Normally, the next instruction is taken from the same process from which the current instruction was executed; occasionally, interrupts from I/O devices or internal timers will cause the execution to be interrupted. A new process called an interrupt handler will be executed, and upon its completion, an operating system function called the scheduler may be invoked to select a new process to execute.

This mechanism is called a context switch. The diagram below shows the memory divided into five segments, one for the operating system code and data, and four for the code and data of the programs that are running concurrently:

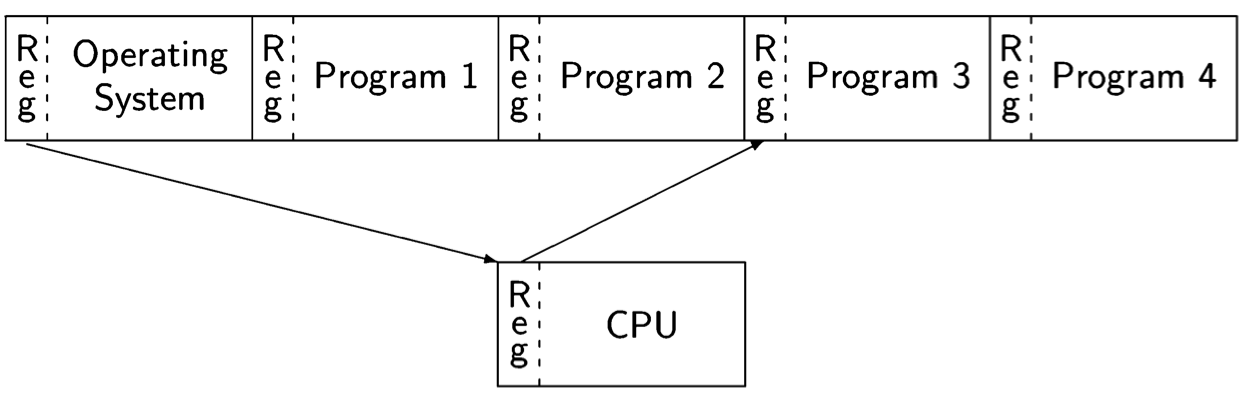
When the execution is interrupted, the registers in the CPU (not only the registers used for computation, but also the control pointer and other registers that point to the memory segment used by the program) are saved into a prespecified area in the program’s memory. Then the register contents required to execute the interrupt handler are loaded into the CPU. At the conclusion of the interrupt processing, the symmetric context switch is performed, storing the interrupt handler registers and loading the registers for the program. The end of interrupt processing is a convenient time to invoke the operating system scheduler, which may decide to perform the context switch with another program, not the one that was interrupted.

In a multitasking system, the non-intuitive aspect of the abstraction is not the in- terleaving of atomic statements (that actually occurs), but the requirement that any arbitrary interleaving is acceptable. After all, the operating system scheduler may only be called every few milliseconds, so many thousands of instructions will be executed from each process before any instructions are interleaved from another. We defer a discussion of this important point to Section 2.4.

Multiprocessor computers

A multiprocessor computer is a computer with more than one CPU. The memory is physically divided into banks of local memory, each of which can be accessed only by one CPU, and global memory, which can be accessed by all CPUs:

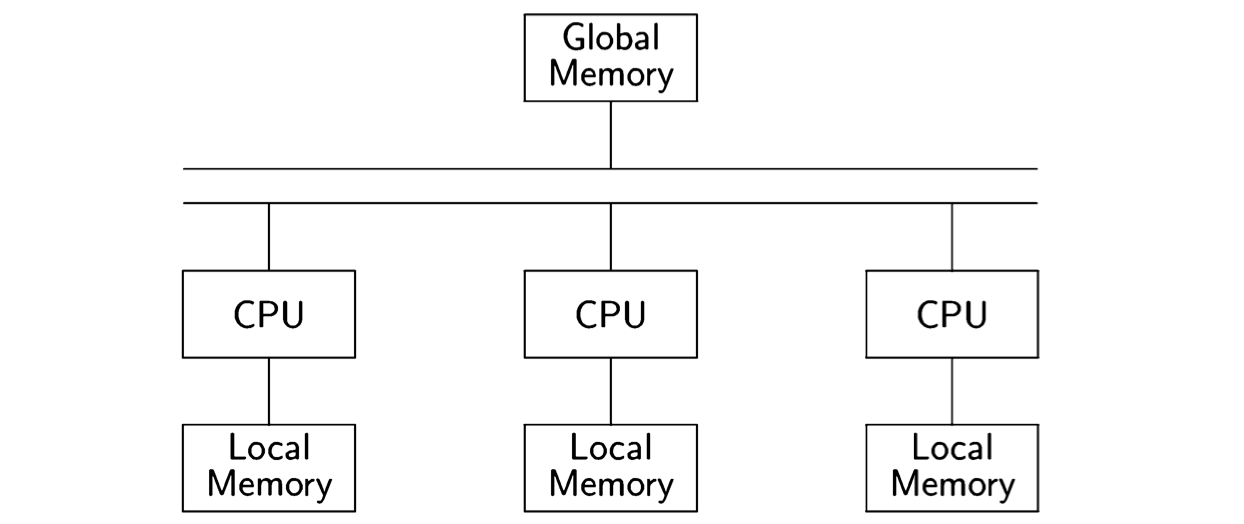
If we have a sufficient number of CPUs, we can assign each process to its own CPU. The interleaving assumption no longer corresponds to reality, since each CPU is executing its instructions independently. Nevertheless, the abstraction is useful here.

As long as there is no contention, that is, as long as two CPUs do not attempt to access the same resource (in this case, the global memory), the computations defined by interleaving will be indistinguishable from those of truly parallel exe- cution. With contention, however, there is a potential problem. The memory of a computer is divided into a large number of cells that store data which is read and written by the CPU. Eight-bit cells are called bytes and larger cells are called words, but the size of a cell is not important for our purposes. We want to ask what might happen if two processors try to read or write a cell simultaneously so that the operations overlap. The following diagram indicates the problem:

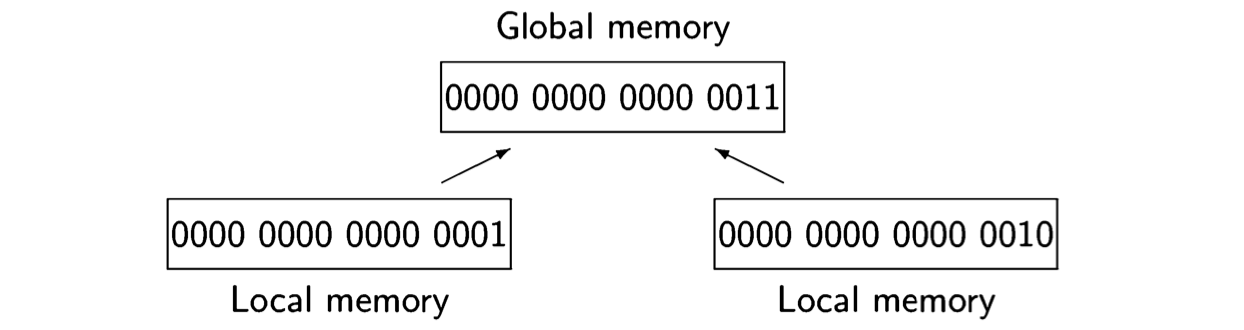
It shows 16-bit cells of local memory associated with two processors; one cell contains the value 0 ... 01 and one contains 0 ... 10 = 2. If both processors write to the cell of global memory at the same time, the value might be undefined; for example, it might be the value 0 ... 11 = 3 obtained by or’ing together the bit representations of 1 and 2.

In practice, this problem does not occur because memory hardware is designed so that (for some size memory cell) one access completes before the other com- mences. Therefore, we can assume that if two CPUs attempt to read or write the same cell in global memory, the result is the same as if the two instructions were executed in either order. In effect, atomicity and interleaving are performed by the hardware.

Other less restrictive abstractions have been studied; we will give one example of an algorithm that works under the assumption that if a read of a memory cell over- laps a write of the same cell, the read may return an arbitrary value (Section 5.3).

The requirement to allow arbitrary interleaving makes a lot of sense in the case of a multiprocessor; because there is no central scheduler, any computation resulting from interleaving may certainly occur.

Distributed systems

A distributed system is composed of several computers that have no global resources; instead, they are connected by communications channels enabling them to send messages to each other. The language of graph theory is used in discussing distributed systems; each computer is a node and the nodes are connected by (di-rected) edges. The following diagram shows two possible schemes for interconnecting nodes: on the left, the nodes are fully connected while on the right they are connected in a ring:

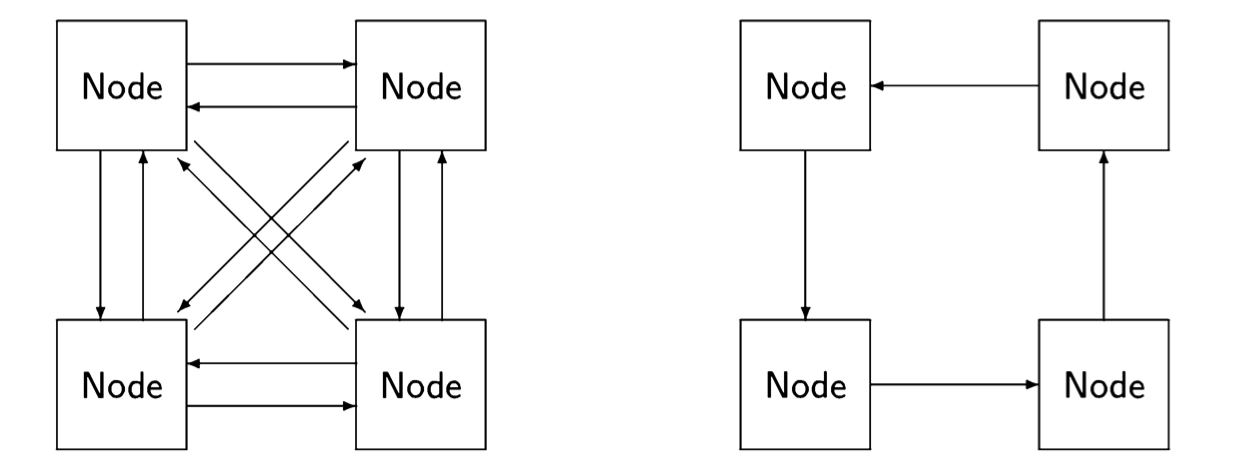
In a distributed system, the abstraction of interleaving is, of course, totally false, since it is impossible to coordinate each node in a geographically distributed sys- tem. Nevertheless, interleaving is a very useful fiction, because as far as each node is concerned, it only sees discrete events: it is either executing one of its own statements, sending a message or receiving a message. Any interleaving of all the events of all the nodes can be used for reasoning about the system, as long as the interleaving is consistent with the statement sequences of each individual node and with the requirement that a message be sent before it is received.

Distributed systems are considered to be distinct from concurrent systems. In a concurrent system implemented by multitasking or multiprocessing, the global memory is accessible to all processes and each one can access the memory efficiently. In a distributed system, the nodes may be geographically distant from each other, so we cannot assume that each node can send a message directly to all other nodes. In other words, we have to consider the topology or connectedness of the system, and the quality of an algorithm (its simplicity or efficiency) may be dependent on a specific topology. A fully connected topology is extremely efficient in that any node can send a message directly to any other node, but it is extremely expensive, because for n nodes, we need $ n · (n-1) \approx n^2 $ communications channels. The ring topology has minimal cost in that any node has only one communications line associated with it, but it is inefficient, because to send a message from one arbitrary node to another we may need to have it relayed through up to $ n - 2 $ other nodes.

A further difference between concurrent and distributed systems is that the behavior of systems in the presence of faults is usually studied within distributed systems. In a multitasking system, hardware failure is usually catastrophic since it affects all processes, while a software failure may be relatively innocuous (if the process simply stops working), though it can be catastrophic (if it gets stuck in an infinite loop at high priority). In a distributed system, while failures can be catastrophic for single nodes, it is usually possible to diagnose and work around a faulty node, because messages may be relayed through alternate communication paths. In fact, the success of the Internet can be attributed to the robustness of its protocols when individual nodes or communications channels fail.

Arbitrary interleaving

We have to justify the use of arbitrary interleavings in the abstraction. What this means, in effect, is that we ignore time in our analysis of concurrent programs. For example, the hardware of our system may be such that an interrupt can occur only once every millisecond. Therefore, we are tempted to assume that several thousand statements are executed from a single process before any statements are executed from another. Instead, we are going to assume that after the execution of any statement, the next statement may come from any process. What is the justification for this abstraction?

The abstraction of arbitrary interleaving makes concurrent programs amenable to formal analysis, and as we shall see, formal analysis is necessary to ensure the correctness of concurrent programs. Arbitrary interleaving ensures that we only have to deal with finite or countable sequences of statements $ a_1,a_2,a_3, \dots,$ and need not analyze the actual time intervals between the statements. The only relation between the statements is that a; precedes or follows (or immediately precedes or follows) $a_j$. Remember that we did not specify what the atomic statements are, so you can choose the atomic statements to be as coarse-grained or as fine-grained as you wish. You can initially write an algorithm and prove its correctness under the assumption that each function call is atomic, and then refine the algorithm to assume only that each statement is atomic.

The second reason for using the arbitrary interleaving abstraction is that it enables us to build systems that are robust to modification of their hardware and software. Systems are always being upgraded with faster components and faster algorithms. If the correctness of a concurrent program depended on assumptions about time of execution, every modification to the hardware or software would require that the system be rechecked for correctness (see [62] for an example). For example, suppose that an operating system had been proved correct under the assumption that characters are being typed in at no more than 10 characters per terminal per second. That is a conservative assumption for a human typist, but it would become invalidated if the input were changed to come from a communications channel.

The third reason is that it is difficult, if not impossible, to precisely repeat the execution of a concurrent program. This is certainly true in the case of systems that accept input from humans, but even in a fully automated system, there will always be some jitter, that is some unevenness in the timing of events. A concurrent program cannot be debugged in the familiar sense of diagnosing a problem, correcting the source code, recompiling and rerunning the program to check if the bug still exists. Rerunning the program may just cause it to execute a different scenario than the one where the bug occurred. The solution is to develop programming and verification techniques that ensure that a program is correct under all interleavings.

Atomic statements

The concurrent programming abstraction has been defined in terms of the interleaving of atomic statements. What this means is that an atomic statement is executed to completion without the possibility of interleaving statements from another process. An important property of atomic statements is that if two are executed simultaneously, the result is the same as if they had been executed sequentially (in either order). The inconsistent memory store shown on page 15 will not occur.

It is important to specify the atomic statements precisely, because the correctness of an algorithm depends on this specification. We start with a demonstration of the effect of atomicity on correctness, and then present the specification used in this book.

Recall that in our algorithms, each labeled line represents an atomic statement. Consider the following trivial algorithm:

There are two possible scenarios:

In both scenarios, the final value of the global variable n is 2, and the algorithm is a correct concurrent algorithm with respect to the postcondition $n = 2$.

Now consider a modification of the algorithm, in which each atomic statement references the global variable n at most once:

There are scenarios of the algorithm that are also correct with respect to the post- condition $n = 2$:

As long as p1 and p2 are executed immediately one after the other, and similarly for q1 and q2, the result will be the same as before, because we are simulating the execution of $n\leftarrow n+1$ with two statements. However, other scenarios are possible in which the statements from the two processes are interleaved:

Clearly, Algorithm 2.4 is not correct with respect to the postcondition$n = 2$.

We learn from this simple example that the correctness of a concurrent program is relative to the specification of the atomic statements. The convention in the book is that:

Assignment statements are atomic statements, as are evaluations of boolean conditions in control statements.

This assumption is not at all realistic, because computers do not execute source code assignment and control statements; rather, they execute machine-code instructions that are defined at a much lower level. Nevertheless, by the simple expedient of defining local variables as we did above, we can use this simple model to demonstrate the same behaviors of concurrent programs that occur when machine-code instructions are interleaved. The source code programs might look artificial, but the convention spares us the necessity of using machine code during the study of concurrency. For completeness, Section 2.8 provides more detail on the interleaving of machine-code instructions.

Correctness

In sequential programs, rerunning a program with the same input will always give the same result, so it makes sense to debug a program: run and rerun the program with breakpoints until a problem is diagnosed; fix the source code; rerun to check if the output is not correct. In a concurrent program, some scenarios may give the correct output while others do not. You cannot debug a concurrent program in the normal way, because each time you run the program, you will likely get a different scenario. The fact that you obtain the correct answer may just be a fluke of the particular scenario and not the result of fixing a bug.

In concurrent programming, we are interested in problems—like the problem with Algorithm 2.4—that occur as a result of interleaving. Of course, concurrent programs can have ordinary bugs like incorrect bounds of loops or indices of arrays, but these present no difficulties that were not already present in sequential programming. The computations in examples are typically trivial such as incrementing a single variable, and in many cases, we will not even specify the actual computations that are done and simply abstract away their details, leaving just the name of a procedure, such as critical section. Do not let this fool you into thinking that concurrent programs are toy programs; we will use these simple programs to develop algorithms and techniques that can be added to otherwise correct programs (of any complexity) to ensure that correctness properties are fulfilled in the presence of interleaving.

For sequential programs, the concept of correctness is so familiar that the formal definition is often neglected. (For reference, the definition is given in Appendix B.) Correctness of (non-terminating) concurrent programs is defined in terms of properties of computations, rather than in terms of computing a functional result. There are two types of correctness properties:

Safety properties The property must always be true.

Liveness properties The property must eventually become true.

More precisely, for a safety property P to hold, it must be true that in every state of every computation, P is true. For example, we might require as a safety property of the user interface of an operating system: Always, a mouse cursor is displayed. If we can prove this property, we can be assured that no customer will ever complain that the mouse cursor disappears, no matter what programs are running on the system.

For a liveness property P to hold, it must be true that in every computation there is some state in which P is true. For example, a liveness property of an operating

system might be: If you click on a mouse button, eventually the mouse cursor will change shape. This specification allows the system not to respond immediately to the click, but it does ensure that the click will not be ignored indefinitely.

It is very easy to write a program that will satisfy a safety property. For example, the following program for an operating system satisfies the safety property Always, a mouse cursor is displayed:

while true
    display the mouse cursor

I seriously doubt if you would find users for an operating system whose only feature is to display a mouse cursor. Furthermore, safety properties often take the form of Always, something “bad” is not true, and this property is trivially satisfied by an empty program that does nothing at all. The challenge is to write concurrent programs that do useful things—thus satisfying the liveness properties—without violating the safety properties.

Safety and liveness properties are duals of each other. This means that the negation of a safety property is a liveness property and vice versa. Suppose that we want to prove the safety property Always, a mouse cursor is displayed. The negation of this property is a liveness property: Eventually, no mouse cursor will be dis- played. The safety property will be true if and only if the liveness property is false. Similarly, the negation of the liveness property if you click on a mouse button, eventually the cursor will change shape, can be expressed as Once a button has been clicked, always, the cursor will not change its shape. The liveness property is true if this safety property is false. One of the forms will be more natural to use in a specification, though the dual form may be easier to prove.

Because correctness of concurrent programs is defined on all scenarios, it is impossible to demonstrate the correctness of a program by testing it. Formal methods have been developed to verify concurrent programs, and these are extensively used in critical systems.

Linear and branching temporal logics

The formalism we use in this book for expressing correctness properties and veri- fying programs is called linear temporal logic (LTL). LTL expresses properties that must be true at a state in a single (but arbitrary) scenario. Branching temporal logic is an alternate formalism; in these logics, you can express that for a property to be true at state, it must be true in some or all scenarios starting from the state. CTL [24] is a branching temporal logic that is widely used especially in the verification of computer hardware. Model checkers for CTL are SMV and NuSMV. LTL is used in this book both because it is simpler and because it is more appropriate for reasoning about software algorithms.

Fairness

There is one exception to the requirement that any arbitrary interleaving is a valid execution of a concurrent program. Recall that the concurrent programming ab- straction is intended to represent a collection of independent computers whose in- structions are interleaved. While we clearly stated that we did not wish to assume anything about the absolute speeds at which the various processors are executing, it does not make sense to assume that statements from any specific process are never selected in the interleaving.

Definition 2.6 A scenario is (weakly) fair if at any state in the scenario, a statement that is continually enabled eventually appears in the scenario.

If after constructing a scenario up to the ith state $ s_0, s_1, \dots, s_i$, the control pointer of a process p points to a statement pj that is continually enabled, then $p_j$ will appear in the scenario as $ s_k $, for $ k > i $. Assignment and control statements are continually enabled. Later we will encounter statements that may be disabled, as well as other (stronger) forms of fairness.

Consider the following algorithm:

Let us ask the question: does this algorithm necessarily halt? That is, does the algorithm halt for all scenarios? Clearly, the answer is no, because one scenario is $ p_1, p_2, p_1, p_2 \dots$, in which p1 and then p2 are always chosen, and q1 is never chosen. Of course this is not what was intended. Process q is continually ready to run because there is no impediment to executing the assignment to flag, so the non-terminating scenario is not fair. If we allow only fair scenarios, then eventually an execution of q1 must be included in every scenario. This causes process q to terminate immediately, and process p to terminate after executing at most two more statements. We will say that under the assumption of weak fairness, the algorithm is correct with respect to the claim that it always terminates.

Machine-code instructions

Algorithm 2.4 may seem artificial, but it a faithful representation of the actual im- plementation of computer programs. Programs written in a programming language like Ada or Java are compiled into machine code. In some cases, the code is for a specific processor, while in other cases, the code is for a virtual machine like the Java Virtual Machine (JVM). Code for a virtual machine is then interpreted or a further compilation step is used to obtain code for a specific processor. While there are many different computer architectures—both real and virtual—they have much in common and typically fall into one of two categories.

Register machines

A register machine performs all its computations in a small amount of high-speed memory called registers that are an integral part of the CPU. The source code of the program and the data used by the program are stored in large banks of memory, so that much of the machine code of a program consists of load instructions, which move data from memory to a register, and store instructions, which move data from a register to memory. load and store of a memory cell (byte or word) is atomic.

The following algorithm shows the code that would be obtained by compiling Algorithm 2.3 for a register machine:

The notation add R1, #1 means that the value 1 is added to the contents of register R1, rather than the contents of the memory cell whose address is 1.

The following diagram shows the execution of the three instructions:

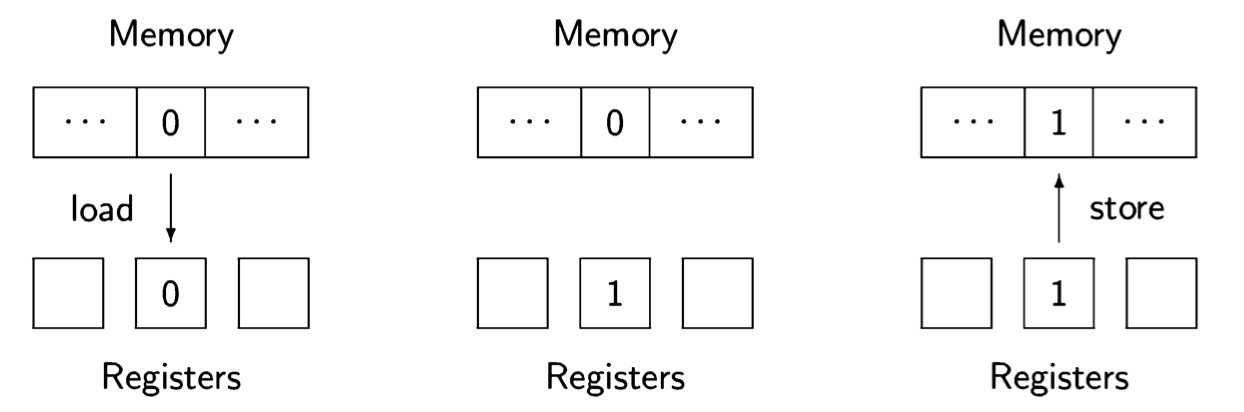
First, the value stored in the memory cell for n is loaded into one of the registers; second, the value is incremented within the register; and third, the value is stored back into the memory cell.

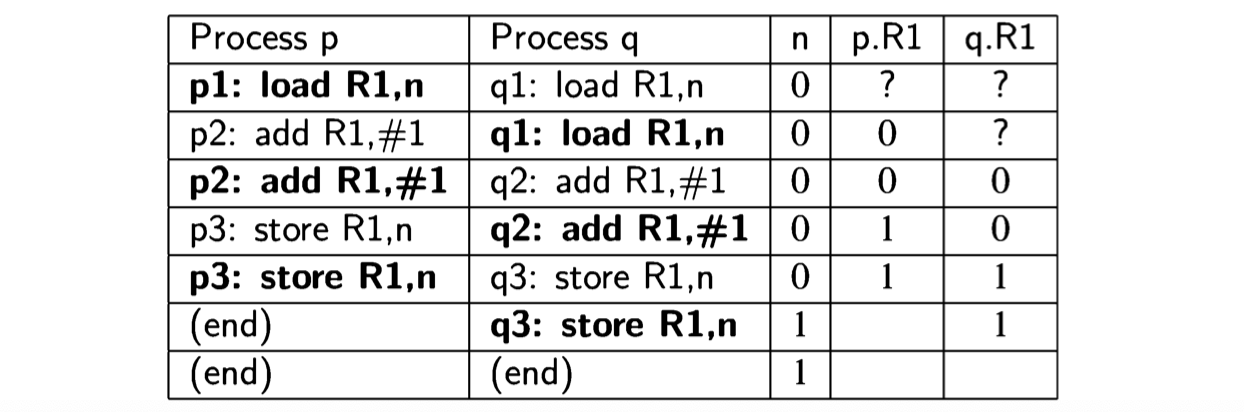
Ostensibly, both processes are using the same register R1, but in fact, each process keeps its own copy of the registers. This is true not only on a multiprocessor or distributed system where each CPU has its own set of registers, but even on a multitasking single-CPU system, as described in Section 2.3. The context switch mechanism enables each process to run within its own context consisting of the current data in the computational registers and other registers such as the control pointer. Thus we can look upon the registers as analogous to the local variables temp in Algorithm 2.4 and a bad scenario exists that is analogous to the bad scenario for that algorithm:

Stack machines

The other type of machine architecture is the stack machine. In this architecture, data is held not in registers but on a stack, and computations are implicitly performed on the top elements of a stack. The atomic instructions include push and pop, as well as instructions that perform arithmetical, logical and control operations on elements of the stack. In the register machine, the instruction add R1,#1 explicitly mentions its operands, while in a stack machine the instruction would simply be written add, and it would add the values in the top two positions in the stack, leaving the result on the top in place of the two operands:

The following diagram shows the execution of these instructions on a stack machine:

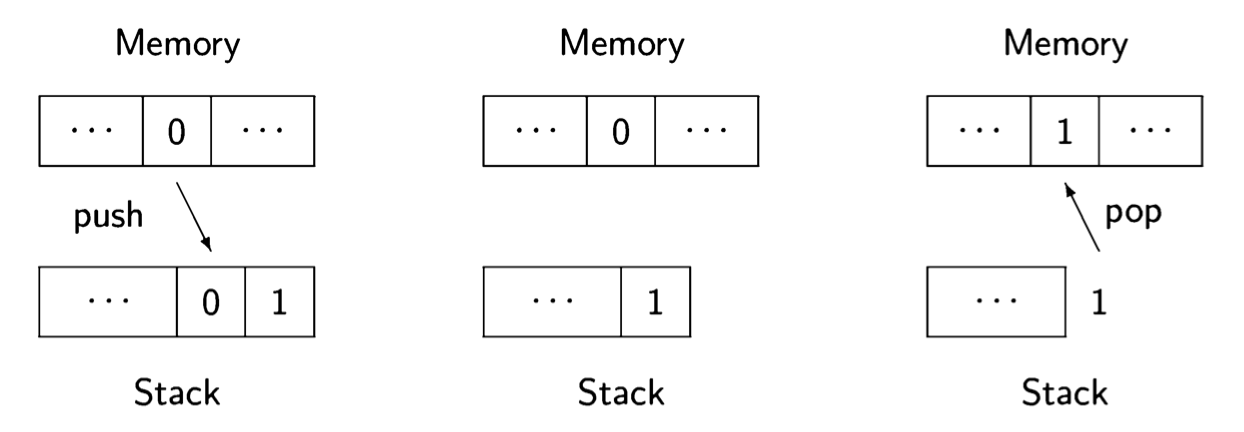
Initially, the value of the memory cell for n is pushed onto the stack, along with the constant 1. Then the two top elements of the stack are added and replaced by one element with the result. Finally (on the right), the result is popped off the stack and stored in the memory cell. Each process has its own stack, so the top of the stack, where the computation takes place, is analogous to a local variable.

It is easier to write code for a stack machine, because all computation takes place in one place, whereas in a register machine with more than one computational register you have to deal with the allocation of registers to the various operands. This is a non-trivial task that is discussed in textbooks on compilation. Furthermore, since different machines have different numbers and types of registers, code for register machines is not portable. On the other hand, operations with registers are extremely fast, whereas if a stack is implemented in main memory access to operands will be much slower.

For these reasons, stack architectures are common in virtual machines where sim- plicity and portability are most important. When efficiency is needed, code for the virtual machine can be compiled and optimized for a specific real machine. For our purposes the difference is not great, as long as we have the concept of memory that may be either global to all processes or local to a single process. Since global and local variables exist in high-level programming languages, we do not need to discuss machine code at all, as long as we understand that some local variables are being used as surrogates for their machine-language equivalents.

Source statements and machine instructions

We have specified that source statements like

\[ n \leftarrow n + 1 \]

are atomic. As shown in Algorithm 2.6 and Algorithm 2.7, such source statements must be compiled into a sequence of machine language instructions. (On some computers n<-n+1 can be compiled into an atomic increment instruction, but this is not true for a general assignment statement.) This increases the number of interleavings and leads to incorrect results that would not occur if the source statement were really executed atomically.

However, we can study concurrency at the level of source statements by decompos- ing atomic statements into a sequence of simpler source statements. This is what we did in Algorithm 2.4, where the above atomic statement was decomposed into the pair of statements:

\[ temp \leftarrow n + 1 \] \[ n \leftarrow temp + 1 \]

The concept of a simple source statement can be formally defined:

Definition 2.7 An occurrence of a variable v is defined to be critical reference: (a) if it is assigned to in one process and has an occurrence in another process, or (b) if it has an occurrence in an expression in one process and is assigned to in another.

A program satisfies the limited-critical-reference (LCR) restriction if each statement contains at most one critical reference.

Consider the first occurrence of n in $n \leftarrow n + 1$. It is assigned to in process p and has (two) occurrences in process q, so it is critical by (a). The second occurrence of n in $n \leftarrow n + 1$ is critical by (b) because it appears in the expression $n+1$ in p and is also assigned to in q. Consider now the version of the statements that uses local variables. Again, the occurrences of n are critical, but the occurrences of temp are not. Therefore, the program satisfies the LCR restriction. Concurrent programs that satisfy the LCR restriction yield the same set of behaviors whether the statements are considered atomic or are compiled to a machine architecture with atomic load and store. See [50, Section 2.2] for more details.

The more advanced algorithms in this book do not satisfy the LCR restriction, but can easily be transformed into programs that do satisfy it. The transformed programs may require additional synchronization to prevent incorrect scenarios, but the additions are simple and do not contribute to understanding the concepts of the advanced algorithms.

Volatile and non-atomic variables

There are further complications that arise from the compilation of high-level languages into machine code. Consider for example, the following algorithm:

The single statement in process q can be interleaved at any place during the ex- ecution of the statements of p. Because of optimization during compilation, the computation in q may not use the most recent value of n. The value of n may be maintained in a register from the assignment in p1 through the computations in p2, p3 and p4, and only actually stored back into n at statement p5. Furthermore, the compiler may re-order p3 and 4 to take advantage of the fact that the value of n+5 needed in p3 is computed in p4.

These optimizations have no semantic effect on sequential programs, but they do in concurrent programs that use global variables, so they can cause programs to be incorrect. Specifying a variable as volatile instructs the compiler to load and store the value of the variable at each use, rather than attempt to optimize away these loads and stores.

Concurrency may also affect computations with multiword variables. A load or store of a full-word variable (32 bits on most computers) is accomplished atomically, but if you need to load or store longer variables (like higher precision numbers), the operation might be carried out non-atomically. A load from another process might be interleaved between storing the lower half and the upper half of a 64-bit variable. If the processor is not able to ensure atomicity for multiword variables, it can be implemented using a synchronization mechanism such as those to be discussed throughout the book. However, these mechanisms can block processes, which may not be acceptable in a real-time system; a non-blocking algorithm for consistent access to multiword variables is presented in Section 13.9.

Concurrency in Java

The Java language has supported concurrency from the very start. However, the concurrency constructs have undergone modification; in particular, several dangerous constructs have been deprecated (dropped from the language). The latest version (1.5) has an extensive library of concurrency constructs java.util.concurrent, designed by a team led by Doug Lea. For more information on this library see the Java documentation and [44]. Lea’s book explains how to integrate concurrency within the framework of object-oriented design and programming a topic not covered in this book.

The Java language supports concurrency through objects of type Thread. You can write your own classes that extend this type as shown in Listing 2.4. Within a class that extends Thread, you have to define a method called run that contains the code to be run by this process. Once the class has been defined, you can define fields of this type and assign to them objects created by allocators (lines 11-12). However, allocation and construction of a Thread object do not cause the thread to run. You must explicitly call the start method on the object (lines 13-14), which in turn will call the run method.

The global variable n is declared to be static so that we will have one copy that is shared by all of the objects declared to be of this class. The main method of the class is used to allocate and initiate the two processes; we then use the join method to wait for termination of the processes so that we can print out the value of n. Invocations of most thread methods require that you catch (or throw) InterruptedException .

If you run this program, you will almost certainly get the answer 20, because it is highly unlikely that there will be a context switch from one task to another during the loop. You can artificially introduce context switches between between the two assignment statements of the loop: static method Thread.yield() causes the currently executing thread to temporarily cease execution, thus allowing other threads to execute.

Since Java does not have multiple inheritance, it is usually not a good idea to extend the class Thread as this will prevent extending any other class. Instead, any class can contain a thread by implementing the interface Runnable:

class Count implements Runnable {
  @override
  public void run() { ... }
}

Threads are created from Runnable objects as follows:

Count count = new Count();
Thread t1 = new Thread(count);

or simply:

Thread tl = new Thread(new Count());

Volatile

A variable can be declared as volatile (Section 2.9):

volatile int n = 0;

Variables of primitive types except long and double are atomic, and long and double are also atomic if they are declared to be volatile. A reference variable is atomic, but that does not mean that the object pointed to is atomic. Similarly, if a reference variable is declared as volatile it does not follow that the object pointed to is volatile. Arrays can be declared as volatile, but not components of an array.

The Critical Section Problem

TL;DR

This chapter introduced the basic concepts of writing a concurrent program to solve a problem. Even in the simplest model of atomic load and store of shared memory, Dekker’s algorithm can solve the critical section problem, although it leaves much to be desired in terms of simplicity and efficiency. Along the journey to Dekker’s algorithm, we have encountered numerous ways in which concurrent programs can be faulty. Since it is impossible to check every possible scenario for faults, state diagrams are an invaluable tool for verifying the correctness of concurrent algorithms.

The next chapter will explore verification of concurrent programming in depth, first using invariant assertions which are relatively easy to understand and use, and then using deductive proofs in temporal logic which are more sophisticated. Finally, we show how programs can be verified using the Spin model checker.

Introduccion

This chapter presents a sequence of attempts to solve the critical section problem for two processes, culminating in Dekker’s algorithm. The synchronization mech- anisms will be built without the use of atomic statements other than atomic load and store. Following this sequence of algorithms, we will briefly present solutions to the critical section problem that use more complex atomic statements. In the next chapter, we will present algorithms for solving the critical section problem for N processes.

Algorithms like Dekker’s algorithm are rarely used in practice, primarily because real systems support higher synchronization primitives like those to be discussed in subsequent chapters (though see the discussion of “fast” algorithms in Section 5.4). Nevertheless, this chapter is the heart of the book, because each incorrect algorithm demonstrates some pathological behavior that is typical of concurrent algorithms. Studying these behaviors within the framework of these elementary algorithms will prepare you to identify and correct them in real systems.

The proofs of the correctness of the algorithms will be based upon the explicit construction of state diagrams in which all scenarios are represented. Some of the proofs are left to the next chapter, because they require more complex tools, in particular the use of temporal logic to specify and verify correctness properties.

The definition of the problem

We start with a specification of the structure of the critical section problem and the assumptions under which it must be solved:

Each of N processes is executing in a infinite loop a sequence of statements that can be divided into two subsequences: the critical section and the non- critical section.
The correctness specifications required of any solution are:
- Mutual exclusion Statements from the critical sections of two or more pro- cesses must not be interleaved.
- Freedom from deadlock If some processes are trying to enter their critical sections, then one of them must eventually succeed.
- Freedom from (individual) starvation If any process tries to enter its crit- ical section, then that process must eventually succeed.
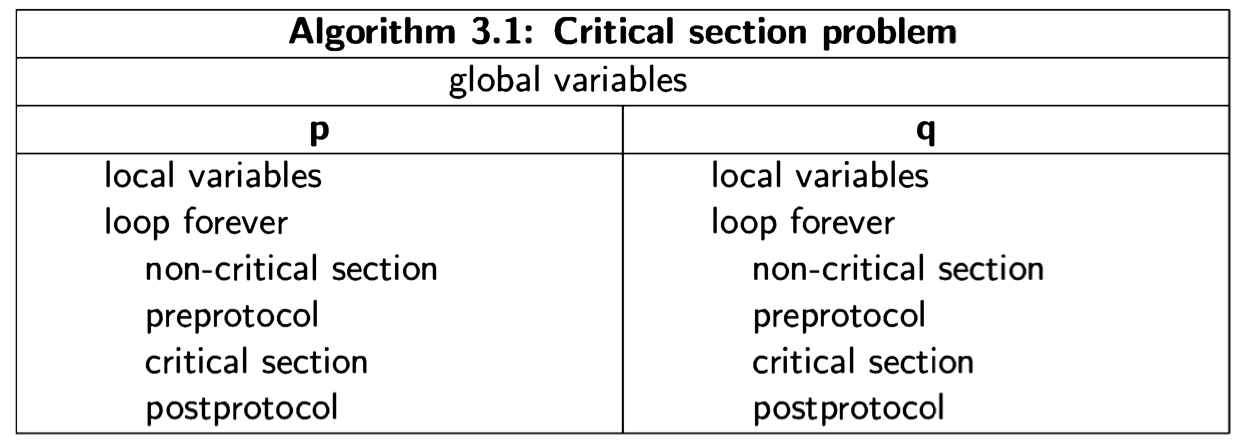
A synchronization mechanism must be provided to ensure that the correctness requirements are met. The synchronization mechanism consists of additional statements that are placed before and after the critical section. The statements placed before the critical section are called the preprotocol and those after it are called the postprotocol. Thus, the structure of a solution for two processes is as follows:
The protocols may require local or global variables, but we assume that no variables used in the critical and non-critical sections are used in the proto- cols, and vice versa.
The critical section must progress, that is, once a process starts to execute the statements of its critical section, it must eventually finish executing those statements.
The non-critical section need not progress, that is, if the control pointer of a process is at or in its non-critical section, the process may terminate or enter an infinite loop and not leave the non-critical section.

The following diagram will help visualize the critical section problem:

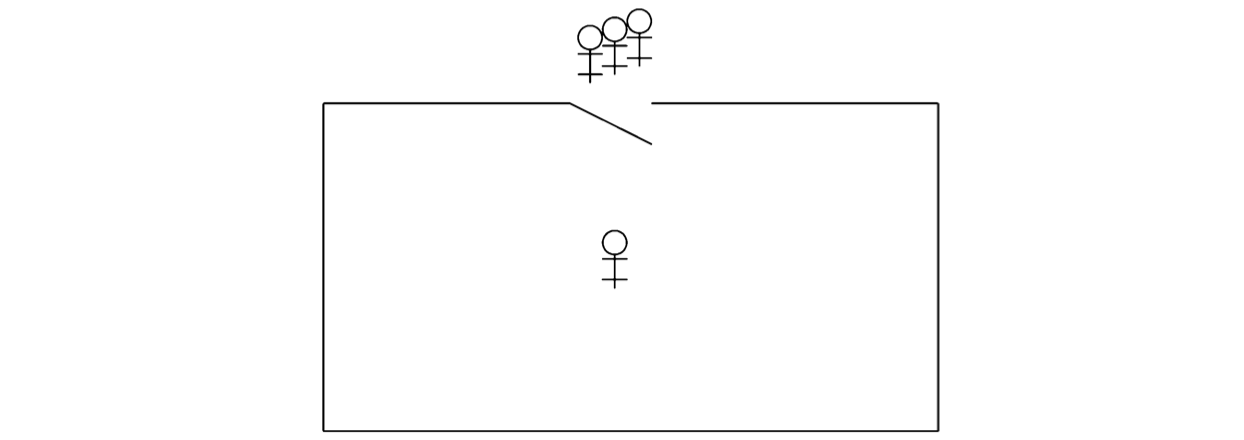
The stick figures represent processes and the box is a critical region in which at most one process at a time may be executing the statements that form its critical section. The solution to the problem is given by the protocols for opening and closing the door to the critical region in such a manner that the correctness properties are satisfied.

The critical section problem is intended to model a system that performs complex computation, but occasionally needs to access data or hardware that is shared by several processes. It is unreasonable to expect that individual processes will never terminate, or that nothing bad will ever occur in the programs of the system. For example, a check-in kiosk at an airport waits for a passenger to swipe his credit card or touch the screen. When that occurs, the program in the kiosk will access a central database of passengers, and it is important that only one of these programs update the database at atime. The critical section is intended to model this operation only, while the non-critical section models all the computation of the program except for the actual update of the database.

It would not make sense to require that the program actually participate in the update of the database by programs in other kiosks, so we allow it to wait indefinitely for input, and we take into account that the program could malfunction. In other words, we do not require that the non-critical section progress. On the other hand, we do require that the critical section progress so that it eventually terminates. The reason is that the process executing a critical section typically holds a lock or permission resource, and the lock or resource must eventually be released so that other processes can enter their critical sections. The requirement for progress is reasonable, because critical sections are usually very short and their progress can be formally verified.

Obviously, deadlock (my computer froze up) must be avoided, because systems are intended to provide a service. Even if there is local progress within the protocols as the processes set and check the protocol variables, if no process ever succeeds in making the transition from the preprotocol to the critical section, the program is deadlocked.

Freedom from starvation is a strong requirement in that it must be shown that no possible execution sequence of the program, no matter how improbable, can cause starvation of any process. This requirement can be weakened; we will see one example in the algorithm of Section 5.4.

A good solution to the critical section problem will also be efficient, in the sense that the pre- and postprotocols will use as little time and memory as possible. In particular, if only a single process wishes to enter its critical section it will succeed in doing so almost immediately.

First attempt

Here is a first attempt at solving the critical section problem for two processes:

The statement await turn=1 is an implementation-independent notation for a statement that waits until the condition turn=1 becomes true. This can be implemented (albeit inefficiently) by a busy-wait loop that does nothing until the condition is true.

The global variable turn can take the two values 1 and 2, and is initially set to the arbitrary value 1. The intended meaning of the variable is that it indicates whose “turn” it is to enter the critical section. A process wishing to enter the critical section will execute a preprotocol consisting of a statement that waits until the value of turn indicates that its turn has arrived. Upon exiting the critical section, the process sets the value of turn to the number of the other process.

We want to prove that this algorithm satisfies the three properties required of a solution to the critical section problem. To that end we first explain the construction of state diagrams for concurrent programs, a concept that was introduced in Section 2.2.

Proving correctness with state diagrams

States

You do not need to know the history of the execution of an algorithm in order to predict the result of the next step to be executed. Let us first examine this claim for sequential algorithms and then consider how it has to be modified for concurrent algorithms. Consider the following algorithm:

Suppose now that the computation has reached statement p2, and the values of a and b are 10 and 20, respectively. You can now predict with absolute certainty that as a result of the execution of statement p2, the value of a will become 150, while the value of b will remain 20; furthermore, the control pointer of the computer will now contain p3. The history of the computation how exactly it got to statement p2 with those values of the variables is irrelevant.

For a concurrent algorithm, the situation is similar:

Suppose that the execution has reached the point where the first process has reached statement p2 and the second has reached q2, and the values of a and b are again 10 and 20, respectively. Because of the interleaving, we cannot predict whether the next statement to be executed will come from process p or from process q; but we can predict that it will be from either one or the other, and we can specify what the outcome will be in either case.

In the sequential Algorithm 3.3, states are triples such as $s_i = (p2, 10,20)$. From the semantics of assignment statements, we can predict that executing the statement p2 in state $s_i$ will cause the state of the computation to change to $s_{i+1} = (p3, 150, 20)$. Thus, given the initial state of the computation $s_0 = (p1, 1, 2)$, we can predict the result of the computation. (If there are input statements, the values placed into the input variables are also part of the state.) It is precisely this property that makes debugging practical: if you find an error, you can set a breakpoint and restart a computation in the same initial state, confident that the state of the computation at the breakpoint is the same as it was in the erroneous computation.

In the concurrent Algorithm 3.4, states are quadruples such as $s*i = (p2, q2, 10, 20)$. We cannot predict what the next state will be, but we can be sure that it is either $s^{p}_{i+1} = (p3, q2, 150, 20) $ or $s^{q}_{i+1} = (p2, q3, 10, 150) $ depending on whether the next state taken is from process p or process q, respectively. While we cannot predict which states will appear in any particular execution of a concurrent algorithm, the set of reachable states (Definition 2.5) are the only states that can appear in any computation. In the example, starting from state s;, the next state will be an element of the set $\{s^{p}_{i+1},s^{q}_{i+1}\}$. From each of these states, there are possibly two new states that can be reached, and so on. To check correctness properties, it is only necessary to examine the set of reachable states and the transitions among them; these are represented in the state diagram.

For the first attempt, Algorithm 3.2, states are triples of the form $(p_i,q_j, turn)$, where turn denotes the value of the variable turn. Remember that we are assuming that any variables used in the critical and non-critical sections are distinct from the variables used in the protocols and so cannot affect the correctness of the solution. Therefore, we leave them out of the description of the state. The mutual exclusion correctness property holds if the set of all accessible states does not contain a state of the form (p3, q3, turn) for some value of turn, because p3 and q3 are the labels of the critical sections.

State diagrams

How many states can there be in a state diagram? Suppose that the algorithm has N processes with $n_i$ statements in process i, and M variables where variable j has $m_j$ possible values. The number of possible states is the number of tuples that can be formed from these values, and we can choose each element of the tuple independently, so the total number of states is $n_1\ x \dots x\ n_N x\ m_1\dots x\ m_M$. For the first attempt, the number of states is $n_1\ x\ n_2\ x\ m_1 = 4\ x\ 4\ x\ 2 = 32$, since it is clear from the text of the algorithm that the variable turn can only have two values, 1 and 2. In general, variables may have as many values as their representation can hold, for example, $2^{32}$ for a 32-bit integer variable.

However, it is possible that not all states can actually occur, that is, it is possible that some states do not appear in any scenario starting from the initial state $s_0 = (p1, q1, 1)$. In fact, we hope so! We hope that the states $(p3, q3, 1)$ and $(p3, q3, 2)$, which violate the correctness requirement of mutual exclusion, are not accessible from the initial state.

To prove a property of a concurrent algorithm, we construct a state diagram and then analyze if the property holds in the diagram. The diagram is constructed in- crementally, starting with the initial state and considering what the potential next states are. If a potential next state has already been constructed, then we can con- nect to it, thus obtaining a finite presentation of an unbounded execution of the algorithm. By the nature of the incremental construction, turn will only have the values 1 and 2, because these are the only values that are ever assigned by the algorithm.

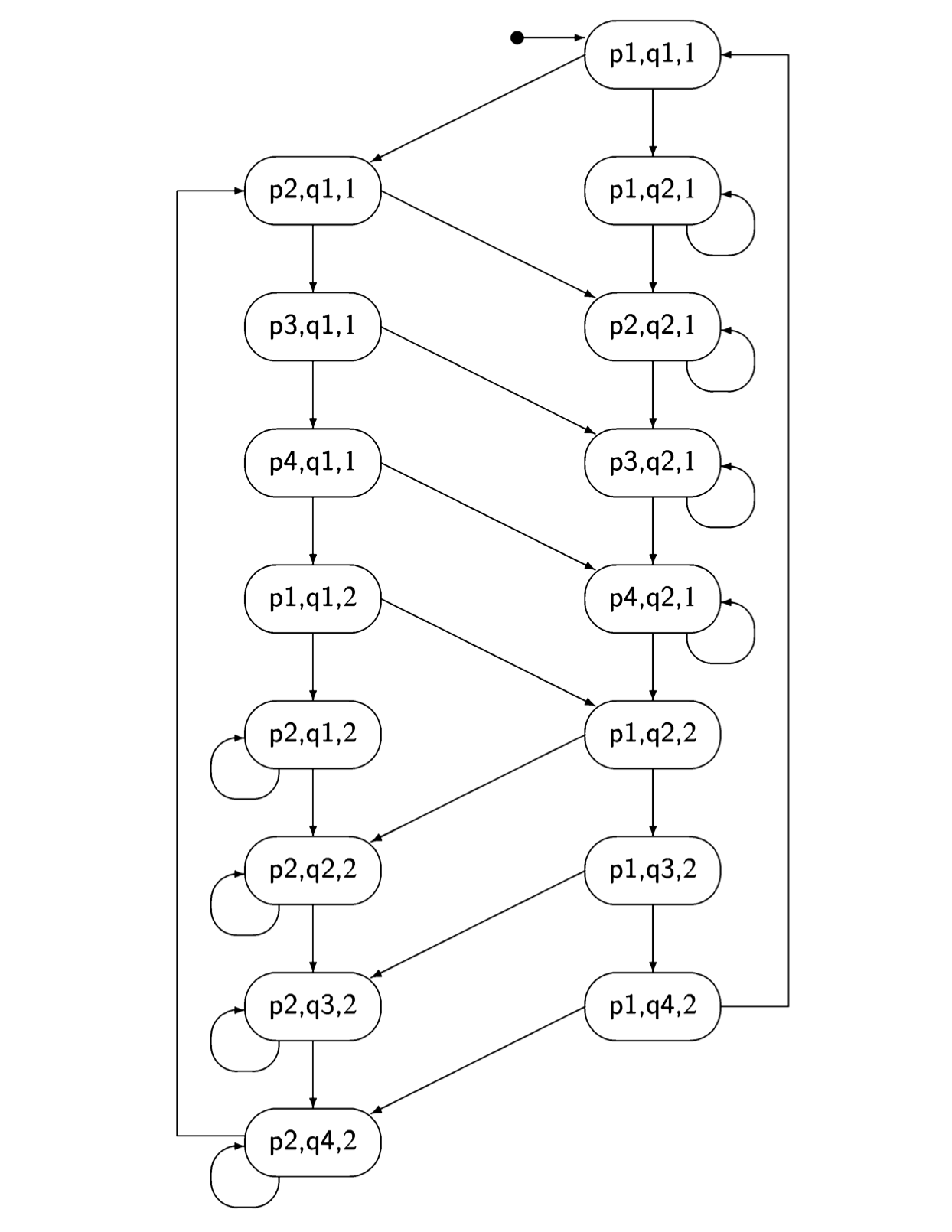
The following diagram shows the first four steps of the incremental construction of the state diagram for Algorithm 3.2:

The initial state is $(p1,q1, 1)$. If we execute pl from process p, the next state is $(p2,q1, 1)$: the first element of the tuple changes because we executed a statement of the first process, the second element does not change because we did not execute a statement of that process, and the third element does not change since by assumption the non critical section does not change the value of the variable turn. If, however, we execute ql from process q, the next state is $(p1, q2, 1)$. From this state, if we try to execute another statement, q2, from process q, we remain in the same state. The statement is await turn=2, but turn = 1. We do not draw another instance of $(p1, q2, 1)$; instead, the arrow representing the transition points to the existing state.

The incremental construction terminates after 16 of the 32 possible states have been constructed, as shown in Figure 3.1. You may (or may not!) want to check if the construction has been carried out correctly.

A quick check shows that neither of the states $(p3, q3, 1)$ nor $(p3, q3, 2)$ occurs; thus we have proved that the mutual exclusion property holds for the first attempt.

Abbreviating the state diagram

Clearly, the state diagram of the simple algorithm in the first attempt is unwieldy. When state diagrams are built, it is important to minimize the number of states that must be constructed. In this case, we can reduce the number of accessible states from 16 to 4, by reducing the algorithm to the one shown below, where we have removed the two statements for the critical and non-critical sections.

Admittedly, this is suspicious. The whole point of the algorithm is to ensure that mutual exclusion holds during the execution of the critical sections, so how can we simply erase these statements? The answer is that whatever statements are executed by the critical section are totally irrelevant to the correctness of the synchronization algorithm.

If in the first attempt, we replace the statement p3: critical section by the com- ment p3: // critical section, the specification of the correctness properties remain unchanged, for example, we must show that we cannot be in either of the states $(p3, q3, 1)$ or $(p3, q3,2)$. But if we are at p3 and that is a comment, it is just as if we were at p4, so we can remove the comment; similar reasoning holds for p1. In the abbreviated first attempt, the critical sections have been swallowed up by $turn \leftarrow 2$ and $turn \leftarrow 1$, and the non-critical sections have been swallowed up by await $turn=1$ and await $turn=2$. The state diagram for this algorithm is shown in Figure 3.2, where for clarity we have given the actual statements and variables names instead of just labels.

Correctness of the first attempt

We are now in a position to try to prove the correctness of the first attempt. As noted above, the proof that mutual exclusion holds is immediate from an examination of the state diagram.

Next we have to prove that the algorithm is free from deadlock. Recall that this means that if some processes are trying to enter their critical section then one of them must eventually succeed. In the abbreviated algorithm, a process is trying to

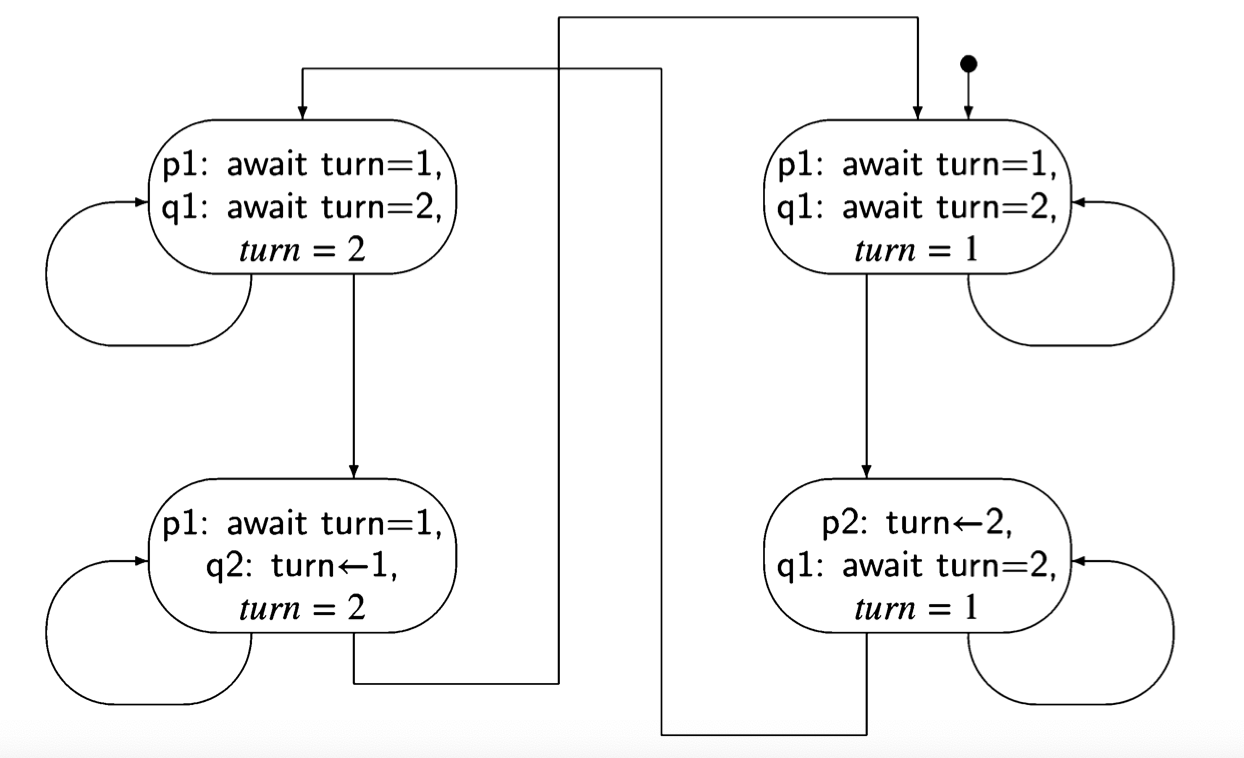
enter its critical section if it is trying to execute its await statement. We have to check this for the four states; since the two left states are symmetrical with the two right states, it suffices to check one of the pairs.

Consider the upper left state (await turn=1, await turn=2, turn = 2). Both pro- cesses are trying to execute their critical sections; if process q tries to execute await turn=2, it will succeed and enter its critical section.

Consider now the lower left state (await $turn=1$, $turn \leftarrow 1$, $turn = 2$). Process p may try to execute await turn=1, but since $turn = 2$, it does not change the state. By the assumption of progress on the critical section and the assignment statement, process q will eventually execute $turn \leftarrow 1$, leading to the upper right state. Now, process p can enter its critical section. Therefore, the property of freedom from deadlock is satisfied.

Finally, we have to check that the algorithm is free from starvation, meaning that if any process is about to execute its preprotocol (thereby indicating its intention to enter its critical section), then eventually it will succeed in entering its critical section. The problem will be easier to understand if we consider the state diagram for the unabbreviated algorithm; the appropriate fragment of the diagram is shown in Figure 3.3, where NCS denotes the non-critical section. Consider the state at the lower left. Process p is trying to enter its critical section by executing p2: await $turn=1$, but since $turn = 2$, the process will loop indefinitely in its await statement until process q executes q4: turn<1. But process q is at q1: NCS and there is No assumption of progress for non-critical sections. Therefore, starvation has occurred: process p is continually checking the value of turn trying to enter its critical section, but process q need never leave its non-critical section, which is necessary if p is to enter its critical section.

Informally, turn serves as a permission resource to enter the critical section, with its value indicating which process holds the resource. There is always some process holding the permission resource, so some process can always enter the critical section, ensuring that there is no deadlock. However, if the process holding the permission resource remains indefinitely in its non-critical section—as allowed by the assumptions of the critical section problem—the other process will never receive the resource and will never enter its critical section. In our next attempt, we will ensure that a process in its non-critical section cannot prevent another one from entering its critical section.

Second attempt

The first attempt was incorrect because both processes set and tested a single global variable. If one process dies, the other is blocked. Let us try to solve the critical section problem by providing each process with its own variable (Algorithm 3.6). The intended interpretation of the variables is that wanti is true from the step where process i wants to enter its critical section until it leaves the critical section. await statements ensure that a process does not enter its critical section while the other process has its flag set. This solution does not suffer from the problem of the

previous one: if a process halts in its non-critical section, the value of its variable want will remain false and the other process will always succeed in immediately entering its critical section.

Let us construct a state diagram for the abbreviated algorithm:

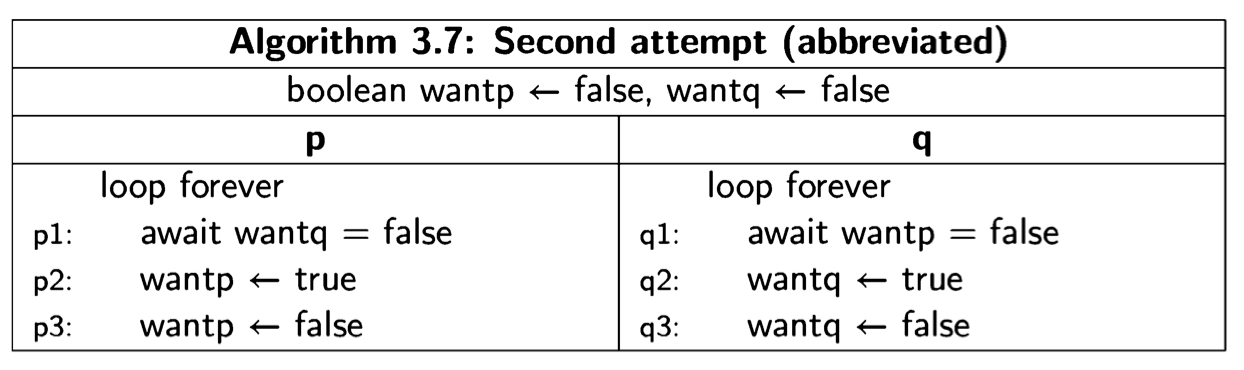
Unfortunately, when we start to incrementally construct the state diagram (Fig- ure 3.4), we quickly find the state (p3: $ wantp \leftarrow false $, q3: $wantq \leftarrow false$, true, true), showing that the mutual exclusion property is not satisfied. (await !want is used instead of await want=false because of space constraints in the node.)

Paths in the state diagram correspond to scenarios; this portion of the scenario can also be displayed in tabular form:

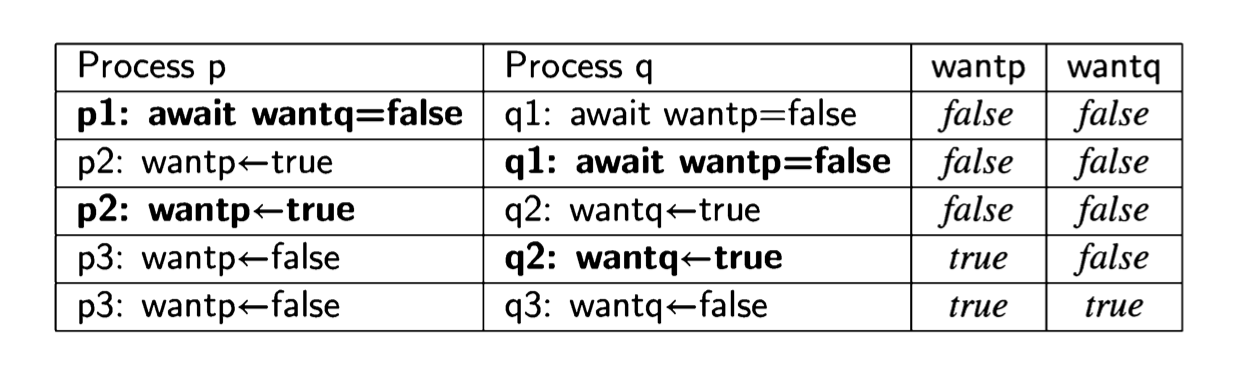
To prove that mutual exclusion holds, we must check that no forbidden state appears in any scenario. So if mutual exclusion does in fact hold, we need to construct

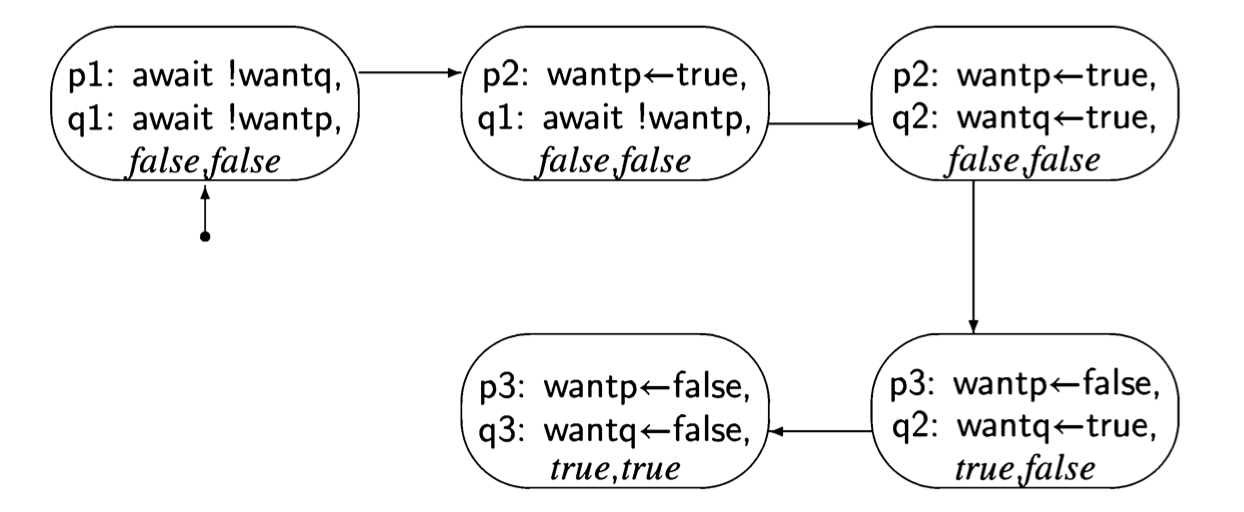
the full state diagram for the algorithm, because every path in the diagram is a sce- nario; then we must examine every state to make sure that it is not a forbidden state. When constructing the diagram incrementally, we check each state as it is created, so that we can stop the construction if a forbidden state is encountered, as it was in this case. It follows that if the incremental construction is completed (that is, there are no more reachable states), then we know that no forbidden states occur.

Third attempt

In the second attempt, we introduced the variables want that are intended to indicate when a process is in its critical section. However, once a process has successfully completed its await statement, it cannot be prevented from entering its critical section. The state reached after the await but before the assignment to want is effectively part of the critical section, but the value of want does not indicate this fact. The third attempt (Algorithm 3.8) recognizes that the await statement

should be considered part of the critical section by moving the assignment to want to before the await. We leave it as an exercise to construct the state diagram for this algorithm, and to show that no state in the diagram violates mutual exclusion. In Section 4.2, we will use logic to prove deductively that the algorithm satisfies the mutual exclusion property.

Unfortunately, the algorithm can deadlock as shown by the following scenario:

This can also be seen in the following fragment of the state diagram:

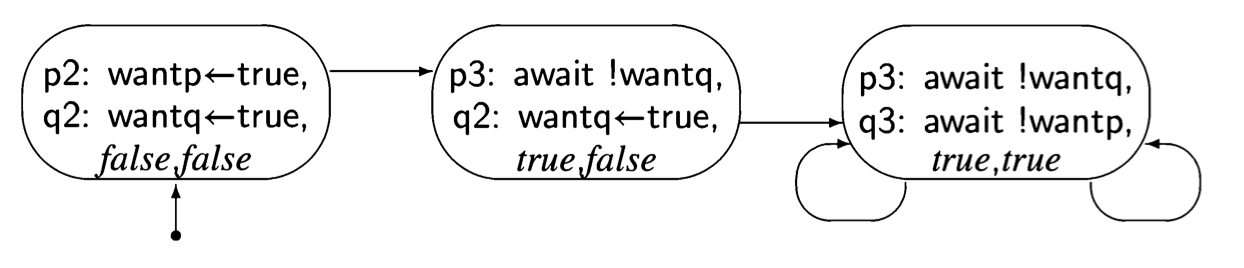
In the rightmost state, both process are trying to enter the critical section, but nei- ther will ever do so, which is our definition of deadlock.

The term deadlock is usually associated with a frozen computation where noth- ing whatsoever is being computed; the situation here—a scenario where several processes are actively executing

Fourth attempt

In the third attempt, when a process sets the variable want to true, not only does it indicate its intention to enter its critical section, but also insists on its right to do so. Deadlock occurs when both processes simultaneously insist on entering their critical sections. The fourth attempt to solve the critical section problem tries to remedy this problem by requiring a process to give up its intention to enter its critical section if it discovers that it is contending with the other process (Algorithm 3.9). The assignment p4: $wantp\leftarrow false$ followed immediately by an assignment to the same variable p5: $wantp\leftarrow true$ would not be meaningful in a sequential algorithm, but

it can be useful in a concurrent algorithm. Since we allow arbitrary interleaving of statements from the two processes, the second process may execute an arbitrary number of statements between the two assignments to wantp. When process p relinquishes the attempt to enter the critical section by resetting wantp to false, process q may now execute the await statement and succeed in entering its critical section.

A State diagram or deductive proof will show that the mutual exclusion property is satisfied and that there is no deadlock. However, a scenario for starvation exists as shown by the cycle in Figure 3.5. The interleaving is “perfect” in the sense that the execution of a statement by process q is always followed immediately by the execution of the equivalently-numbered statement in process p. In this scenario, both processes are starved.

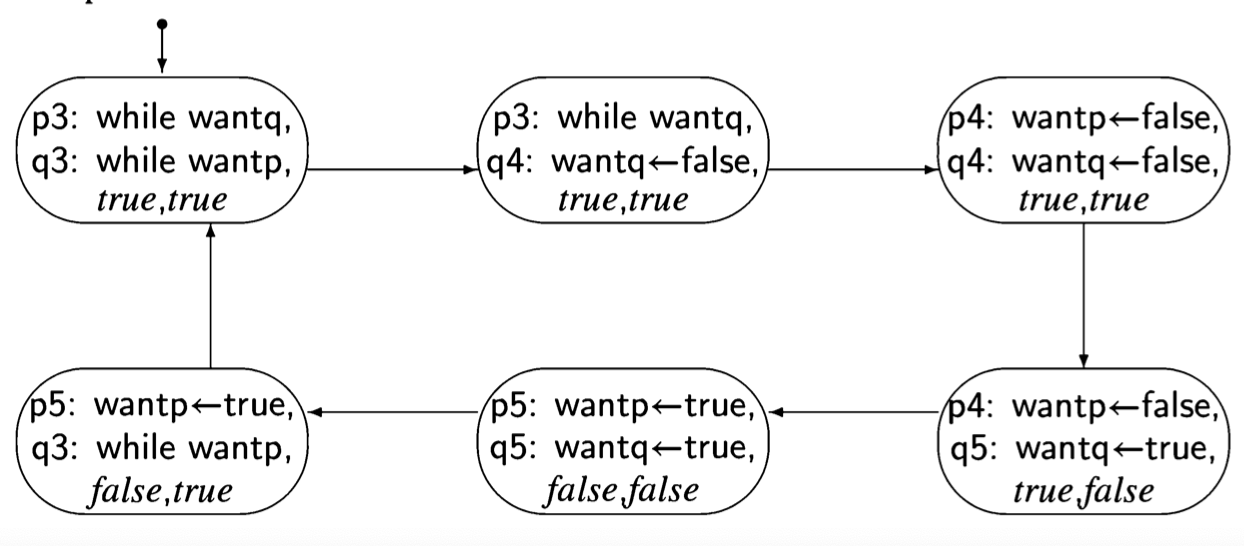
At this point, most people object that this is not a “realistic” scenario; we can hardly expect that whatever is causing the interleaving can indefinitely ensure that exactly two statements are executed by process q followed by exactly two statements from p. But our model of concurrency does not take probability into account. Unlikely scenarios have a nasty way of occurring precisely when a bug would have the most dangerous and costly effects. Therefore, we reject this solution, because it does not fully satisfy the correctness requirements.

Dekker's algorithm

Dekker’s algorithm for solving the critical section problem is a combination of the first and fourth attempts:

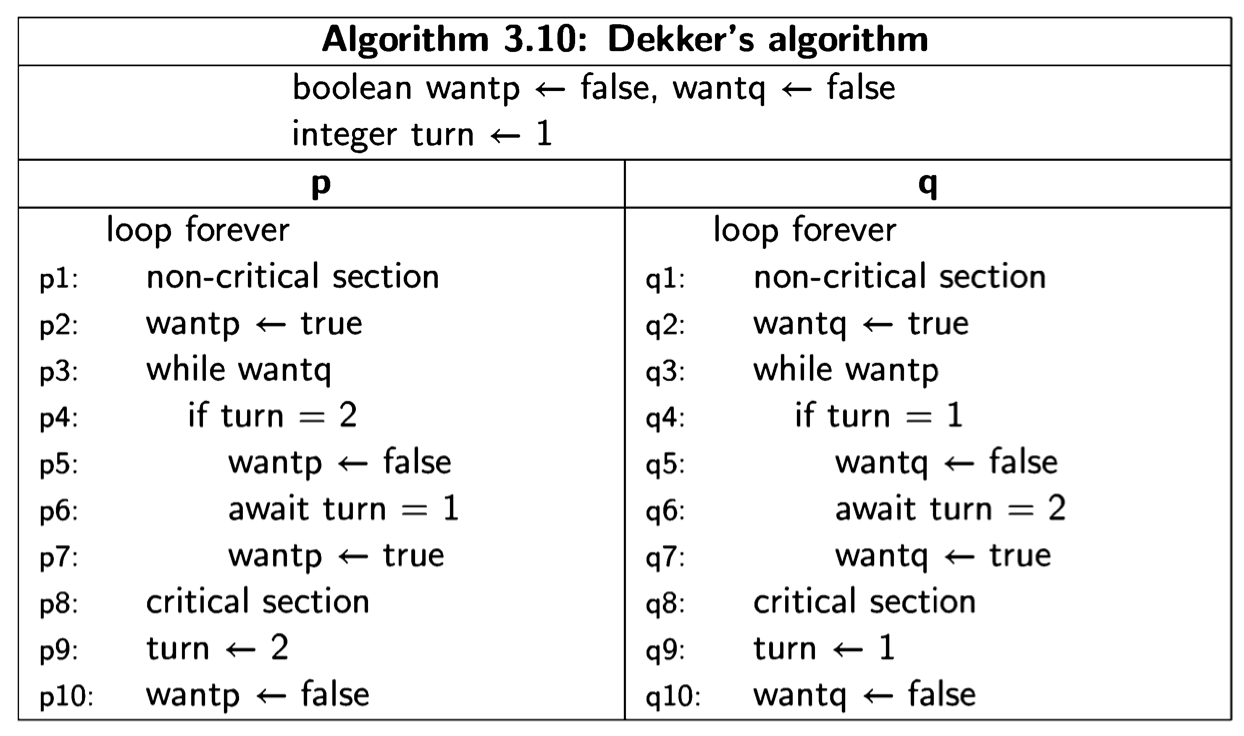
Recall that in the first attempt we explicitly passed the right to enter the critical section between the processes. Unfortunately, this caused the processes to be too closely coupled and prevented correct behavior in the absence of contention. In the fourth attempt, each process had its own variable which prevented problems in the absence of contention, but in the presence of contention both processes insist on entering their critical sections.

Dekker’s algorithm is like the fourth attempted solution, except that the right to insist on entering, rather than the right to enter, is explicitly passed between the processes. The individual variables wantp and wantq ensure mutual exclusion.

Suppose now that process p detects contention by finding wantq to be true at state- ment p3: while wantq. Process p will now consult the global variable turn to see if it is its turn to insist upon entering its critical section ($turn \neq 2$, that is, $turn = 1$). If so, it executes the loop at p3 and p4 until process q resets wantq to false, either by terminating its critical section at q10 or by deferring in q5. If not, process p will reset wantp to false and defer to process q, waiting until that process changes the value of turn after executing its critical section.

Dekker’s algorithm is correct: it satisfies the mutual exclusion property and it is free from deadlock and starvation. The correctness properties by can be proved by constructing and analyzing a state diagram, but instead we will give a deductive proof in Section 4.5.

Semaphores

The algorithms for the critical section problem described in the previous chapters can be run on a bare machine, that is, they use only the machine language instructions that the computer provides. However, these instructions are too low-level to be used efficiently and reliably. In this chapter, we will study the semaphore, which provides a concurrent programming construct on a higher level than machine instructions. Semaphores are usually implemented by an underlying operating system, but we will investigate them by defining the required behavior and assuming that this behavior can be efficiently implemented.

Semaphores are a simple, but successful and widely used, construct, and thus worth exploring in great detail. We start with a section on the concept of process state. Then we define the semaphore construct and show how it trivially solves the critical section problem that we worked so hard to solve in the previous chapters. Section 6.4 defines invariants on semaphores that can be used to prove correctness properties. The next two sections present new problems, where the requirement is not to achieve mutual exclusion but rather cooperation between processes.

Semaphores can be defined in various ways, as discussed in Section 6.8. Section 6.9 introduces Dijkstra’s famous problem of the dining philosophers; the problem is of little practical importance, but it is an excellent framework in which to study concurrent programming techniques. The next two sections present advanced algorithms by Barz and Udding that explore the relative strength of different definitions of semaphores. The chapter ends with a discussion of semaphores in various programming languages.

TL;DR

Semaphores are an elegant and efficient construct for solving problems in concurrent programming. Semaphores are a popular construct, implemented in many systems and easily simulated in others. However, before using semaphores you must find out the precise definition that has been implemented, because the liveness of a program can depend on the specific semaphore semantics.

Despite their popularity, semaphores are usually relegated to low-level programming because they are not structured. Variants of the monitor construct described in the next chapter are widely used because they enable encapsulation of synchronization.

Process state

A multiprocessor system may have more processors than there are processes in a program. In that case, every process is always running on some processor. In a multitasking system (and similarly in a multiprocessor system in which there are more processes than processors), several processes will have to share the computing resources of a single CPU. A process that “wants to” run, that is, a process that can execute its next statement, is called a ready process. At any one time, there will be one running process and any number of ready processes. (If no processes are ready to run, an idle process will be run.)

A system program called a scheduler is responsible for deciding which of the ready processes should be run, and performing the context switch, replacing a running process with a ready process and changing the state of the running process to ready. Our model of concurrency by interleaving of atomic statements makes no assumptions about the behavior of a scheduler; arbitrary interleaving simply means that the scheduler may perform a context switch at any time, even after executing a single statement of arunning process. The reader is referred to textbooks on operating systems [60, 63] for a discussion of the design of schedulers.

Within our model, we do not explicitly mention the concept of a scheduler. However, it is convenient to assume that every process p has associated with it an attribute called its state, denoted p.state. Assignment to this attribute will be used to indicate a change in the state of a process. For example, if p.state = running and q.state = ready, then a context switch between them can be denoted by:

\[ p.state \leftarrow ready \] \[ q.state \leftarrow running \]

The synchronization constructs that we will define assume that there exists another process state called blocked. When a process is blocked, it is not ready so it is not a candidate for becoming the running process. A blocked process can be unblocked or awakened or released only if an external action changes the process state from blocked to ready. At this point the unblocked process becomes a candidate for execution along with all the current ready processes; with one exception (Section 7.5), an unblocked process will not receive any special treatment that would make it the new running process. Again, within our model we do not describe the implementation of the actions of blocking and unblocking, and simply assume that they happen as defined by the synchronization primitives. Note that the await statement does not block a process; it is merely a shorthand for a process that is always ready, and may be running and checking the truth of a boolean expression.

The following diagram summarizes the possible state changes of a process:

Initially, a process is inactive. At some point it is activated and its state becomes ready. When a concurrent program begins executing, one process is running and the others are ready. While executing, it may encounter a situation that requires the process to cease execution and to become blocked until it is unblocked and returns to the ready state. When a process executes its final statement it becomes completed.

In the BACI concurrency simulator, activation of a process occurs when the coend statement is executed. The activation of concurrent processes in languages such as Ada and Java is somewhat more complicated, because it must take into account the dependency of one process on another.

Definition of the semaphore type

A semaphore S is a compound data type with two fields, S.V of type non-negative integer, and S.L of type set of processes. We are using the familiar dotted notation of records and structures from programming languages. A semaphore S must be initialized with a value $ k > 0 $ for S.V and with the empty set $ \emptyset $ for the S.L:

\[semaphore \leftarrow (k, \emptyset) \]

There are two atomic operations defined on a semaphore S (where p denotes the process that is executing the statement):

wait(S)

if S.V > 0
  S.V <- S.V -1
else
  S.L <- S.L U p
  p.state <- blocked

If the value of the integer component is nonzero, decrement its value (and the process p can continue its execution); otherwise it is zero process p is added to the set component and the state of p becomes blocked. We say that p is blocked on the semaphore S.

signal(S)

if S.L = ø
  S.V <- S.V + 1
else
  let q be an arbitrary element of S.L
  S.L <- S.L - {q}
  q.state <- ready

If S.L is empty, increment the value of the integer component; otherwise S.L is nonempty unblock q, an arbitrary element of the set of processes blocked on S.L. The state of process p does not change.

A semaphore whose integer component can take arbitrary non-negative values is called a general semaphore. A semaphore whose integer component takes only the values 0 and 1 is called a binary semaphore. A binary semaphore is initialized with (0, ø) or (1, ø). The wait(S) instruction is unchanged, but signal(S) is now defined by:

if S.v = 1
  // undefined
else if S.L = ø
  S.V <- 1
else // (as above)
  let q be an arbitrary element of S.L
  S.L <- S.L - {q}
  q.state <- ready

A binary semaphore is sometimes called a mutex. This term is used in pthreads and in java.util.concurrent.

Once we have become familiar with semaphores, there will be no need to explicitly write the set of blocked processes S.L.

The critical section problem for two processes

Using semaphores, the solution of the critical section problem for two processes is trivial (Algorithm 6.1). A process, say p, that wishes to enter its critical section executes a preprotocol that consists only of the wait(S) statement. If S.V = 1 then S.V is decremented and p enters its critical section. When p exits its critical section and executes the postprotocol consisting only of the signal(S) statement, the value of S.V will once more be set to 1.

If q attempts to enter its critical section by executing wait(S) before p has left, S.V = 0 and q will become blocked on S. S, the value of the semaphore S, will become (0, {q}). When p leaves the critical section and executes signal(S), the arbitrary process in the set S.L = {q} will be q, so that process will be unblocked and can continue into its critical section.

The solution is similar to Algorithm 3.6, the second attempt, except that the definition of the semaphore operations as atomic statements prevents interleaving between the test of S.V and the assignment to S.V.

To prove the correctness of the solution, consider the abbreviated algorithm where the non-critical section and critical section statements have been absorbed into the following wait(S) and signal(S) statements, respectively.

The state diagram for this algorithm is shown in Figure 6.1. Look at the state in the top center, which is reached if initially process p executes its wait statement, successfully entering the critical section. If process q now executes its wait statement, it finds S.V = 0, so the process is added to S.L as shown in the top right state. Since q is blocked, there is no outgoing arrow for q, and we have labeled the only arrow by p to emphasize that fact. Similarly, in the bottom right state, p is blocked and only process q has an outgoing arrow.

A violation of the mutual exclusion requirement would be a state of the form (p2: signal(S), q2: signal(S), ...). We immediately see that no such state exists, so we conclude that the solution satisfies this requirement. Similarly, there is no deadlock, since there are no states in which both processes are blocked. Finally,

the algorithm is free from starvation, since if a process executes its wait statement (thus leaving the non-critical section), it enters either the state with the signal statement (and the critical section) or it enters a state in which it is blocked. But the only way out of a blocked state is into a state in which the blocked process continues with its signal statement.

Semaphore invariants

Let k be the initial value of the integer component of the semaphore, $signal(S)$ the number of $signal(S)$ statements that have been executed and $wait(S)$ the number of $wait(S)$ statements that have been executed. (A process that is blocked when executing $wait(S)$ is not considered to have successfully executed the statement.)

Theorem 6.1 A semaphore S satisfies the following invariants:

\[ S.V \geq 0 \] \[ S.V = k · singnals(S) - wait(S) \]

Proof: By definition of a semaphore, $k > 0$, so 6.1 is initially true, as is 6.2 since $signal(S)$ and $wait(S)$ are zero. By assumption, non semaphore operations cannot change the value of (either component of) a semaphore, so we only need consider the effect of the wait and signal operations. Clearly, 6.1 is invariant under both operations. If either operation changes S.V, the truth of 6.2 is preserved: If a wait operation decrements S.V, then $wait(S)$ is incremented, and similarly a signal operation that increments S.V also increments $signal(S)$. If a signal operation unblocks a blocked process, S.V is not changed, but both $signal(S)$ and $wait(S)$ increase by one so the righthand side of 6.2 is not changed.

Theorem 6.2 The semaphore solution for the critical section problem is correct: there is mutual exclusion in the access to the critical section, and the program is free from deadlock and starvation.

Proof: Let #CS be the number of processes in their critical sections. We will prove that

\[ CS + SV = 1 \]

is invariant. By a trivial induction on the structure of the program it follows that

\[ CS = wait(S) - signal(S) \]

is invariant. But invariant (6.2) for the initial value k = 1 can be written $wait(S) - signal(S) = 1 - S.V$, so it follows that $CS = 1 - S.V$ is invariant, and this can be written as $CS + S.V = 1$.

Since $S.V > 0$ by invariant (6.1), simple arithmetic shows that $CS < 1$, which proves the mutual exclusion property.

For the algorithm to enter deadlock, both processes must be blocked on the wait statement and $S.V = 0$ Since neither process is in the critical section, $CS = 0$. Therefore $CS + S.V = 0$, which contradicts invariant (6.3).

Suppose that some process, say p, is starved. It must be indefinitely blocked on the semaphore so $S = (0,.S.L)$, where p is in the list S.L. By invariant (6.3), $CS = 1 - S.V = 1 - 0 = 1$, so the other process q is in the critical section. By progress, q will complete the critical section and execute $signal(S)$. Since there are only two processes in the program, S.L must equal the singleton set {p}, so p will be unblocked and enter its critical section.

The critical section problem for N processes

Using semaphores, the same algorithm gives a solution for the critical section problem for N processes:

The proofs in Theorem 6.2 remain unchanged for N processes as far as mutual exclusion and freedom from deadlock are concerned. Unfortunately, freedeom from starvation does not hold. For the abbreviated algorithm:

consider the following scenario for three processes, where the statement numbers for processes q and r correspond to those for p in Algorithm 6.4:

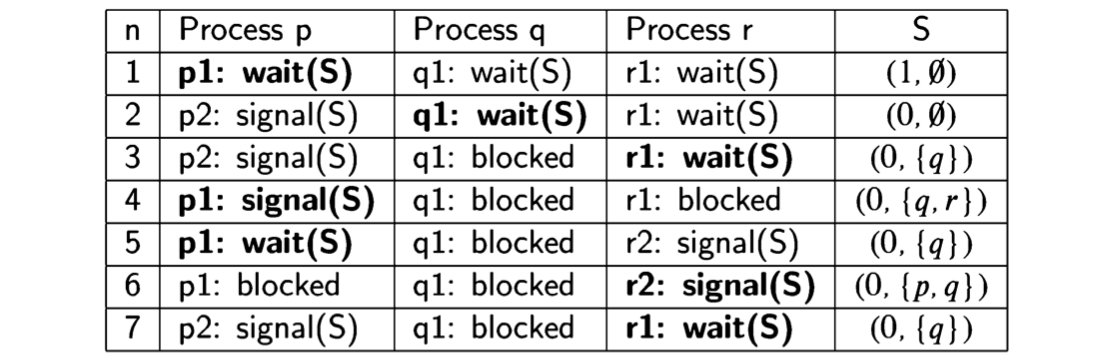
Line 7 is the same as line 3 and the scenario can continue indefinitely in this loop of states. The two processes p and r conspire to starve process q.

When there were only two processes, we used the fact that S.L is the singleton set {p} to claim that process p must be unblocked, but with more than two processes this claim no longer holds. Starvation is caused by the fact that, in our definition of the semaphore type, a signal operation may unblock an arbitrary element of S.L. Freedom from starvation does not occur if the definition of the semaphore type is changed so that S.L is a queue not a set. (See Section 6.8 for a comparison of semaphore definitions.)

In the exercises, you are asked to show that if the initial value of S.V is k, then at most k processes can be in the critical section at any time.

Order of execution problems

The critical section problem is an abstraction of synchronization problems that occur when several processes compete for the same resource. Synchronization problems are also common when processes must coordinate the order of execution of operations of different processes. For example, consider the problem of the concurrent execution of one step of the mergesort algorithm, where an array is divided into two halves, the two halves are sorted concurrently and the results are merged together. Thus, to mergesort the array $[5, 1, 10, 7, 4, 3, 12, 8]$, we divide it into two halves $[5, 1, 10, 7]$ and $[4, 3, 12, 8]$, sort them obtaining $[1, 5, 7, 10]$ and $[3, 4, 8, 12]$, respectively, and then merge the two sorted arrays to obtain $[1, 3, 4, 5, 7, 8, 10, 12]$.

To perform this algorithm concurrently, we will use three processes, two for sorting and one for merging. Clearly, the two sort processes work on totally independent data and need no synchronization, while the merge process must not execute its statements until the two other have completed. Here is a solution using two binary semaphores:

The integer components of the semaphores are initialized to zero, so process merge is initially blocked on $1. Suppose that process sort1 completes before process sort2; then sort1 signals $1 enabling merge to proceed, but it is then blocked on semaphore $2. Only when sort2 completes will merge be unblocked and begin executing its algorithm. If sort2 completes before sort1, it will execute signal(S2), but merge will still be blocked on S1 until sort1 completes.

The producer—consumer problem

The producer-consumer problem is an example of an order-of-execution problem. There are two types of processes in this problem:

Producers A producer process executes a statement produce to create a data ele- ment and then sends this element to the consumer processes.

Consumers Upon receipt of a data element from the producer processes, a con- sumer process executes a statement consume with the data element as a pa- rameter.

As with the critical section and non-critical section statements, the produce and consume statements are assumed not to affect the additional variables used for synchronization and they can be omitted in abbreviated versions of the algorithms.

Producers and consumers are ubiquitous in computing systems:

When a data element must be sent from one process to another, the communica- tions can be synchronous, that is, communications cannot take place until both the producer and the consumer are ready to do so. Synchronous communication is discussed in detail in Chapter 8.

More common, however, is asynchronous communications in which the communications channel itself has some capacity for storing data elements. This store, which is a queue of data elements, is called a buffer. The producer executes an append operation to place a data element on the tail of the queue, and the consumer executes a take operation to remove a data element from the head of the queue.

The use of a buffer allows processes of similar average speeds to proceed smoothly in spite of differences in transient performance. It is important to understand that a buffer is of no use if the average speeds of the two processes are very different. For example, if your web browser continually produces and sends more data than your communications line can carry, the buffer will always be full and there is no advantage to using one. A buffer can also be used to resolve a clash in the structure of data. For example, when you download a compressed archive (a zip file), the files inside cannot be accessed until the entire archive has been read.

There are two synchronization issues that arise in the producer-consumer problem: first, a consumer cannot take a data element from an empty buffer, and second, since the size of any buffer is finite, a producer cannot append a data element to a full buffer. Obviously, there is no such thing as an infinite buffer, but if the buffer is very large compared to the rate at which data is produced, you might want to avoid the extra overhead required by a finite buffer algorithm and risk an occasional loss of data. Loss of data will occur when the producer tries to append a data element to a full buffer; either the operation will not succeed, in which case that element is lost, or it will overwrite one of the existing elements in the buffer (see Section 13.6).

Infinite buffers

If there is an infinite buffer, there is only one interaction that must be synchronized: the consumer must not attempt a take operation from an empty buffer. This is an order-of-execution problem like the mergesort algorithm; the difference is that it happens repeatedly within a loop.

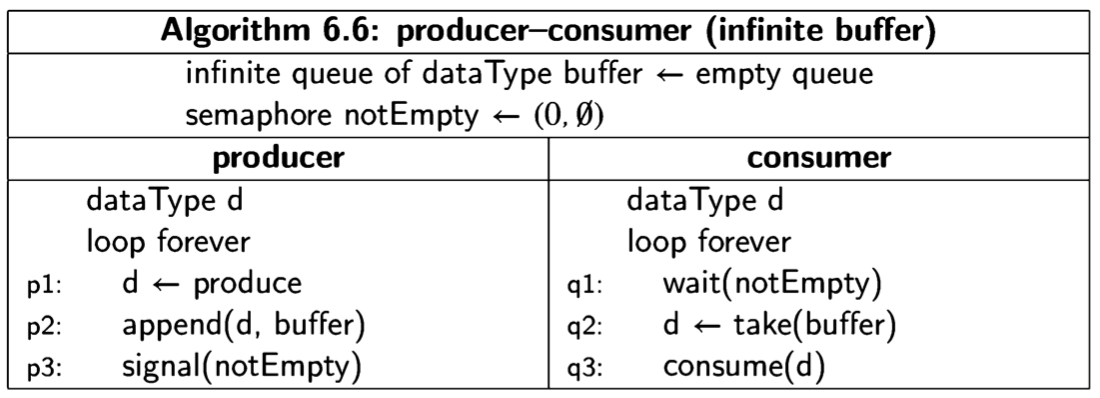
Since the buffer is infinite, it is impossible to construct a finite state diagram for the algorithm. A partial state diagram for the abbreviated algorithm:

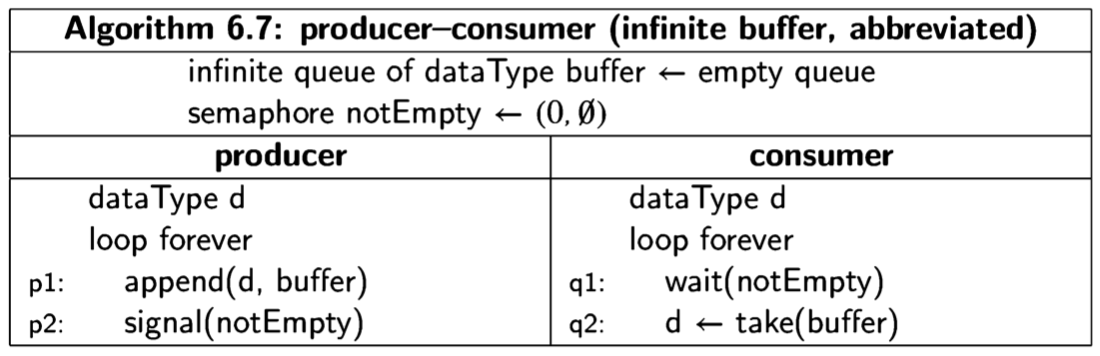
is shown in Figure 6.2. In the diagram, the value of the buffer is written with square brackets and a buffer element is denoted by x; the consumer process is denoted by con. The horizontal arrows indicate execution of operations by the producer, while the vertical arrows are for the consumer. Note that the left two states in the lower row have no arrows for the consumer because it is blocked.

Assume now that the two statements of each process form one atomic statement each. (You are asked to remove this restriction in an exercise.) The following invariant holds:

\[ notEmpty.V = buffer \]

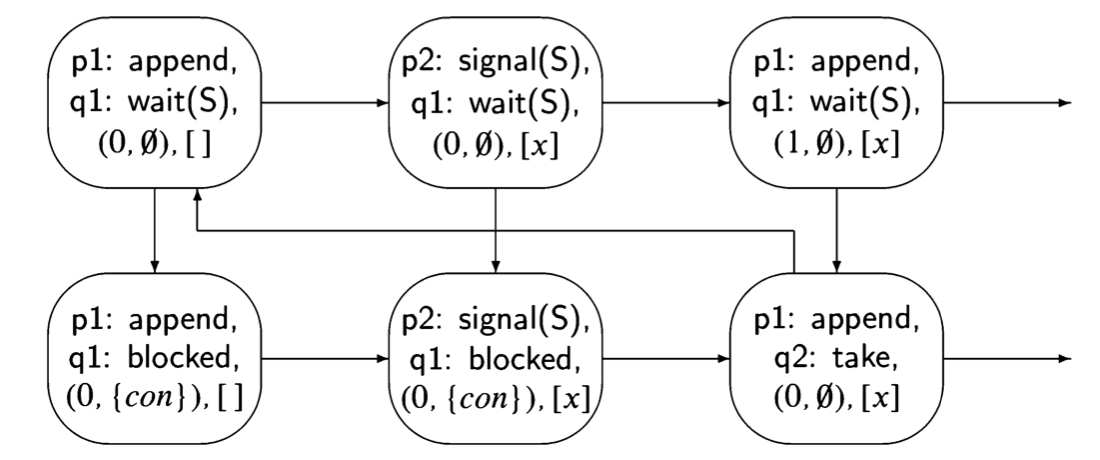
where #buffer is the number of elements in buffer. The formula is true initially since there are no elements in the buffer and the value of the integer component of the semaphore is zero. Each execution of the statements of the producer appends an element to the buffer and also increments the value of notEmpty.V. Each execution of the statements of the consumer takes an element from the buffer and also decrements the value of notEmpty.V. From the invariant, it easily follows that the consumer does not remove an element from an empty buffer.

The algorithm is free from deadlock because as long as the producer continues to produce data elements, it will execute signal(notEmpty) operations and unblock the consumer. Since there is only one possible blocked process, the algorithm is also free from starvation.

Bounded buffers

The algorithm for the producer-consumer problem with an infinite buffer can be easily extended to one with a finite buffer by noticing that the producer takes empty places from the buffer, just as the consumer takes data elements from the buffer (Algorithm 6.8). We can use a similar synchronization mechanism with a semaphore notFull that is initialized to N, the number of (initially empty) places in the finite buffer. We leave the proof of the correctness of this algorithm as an exercise.

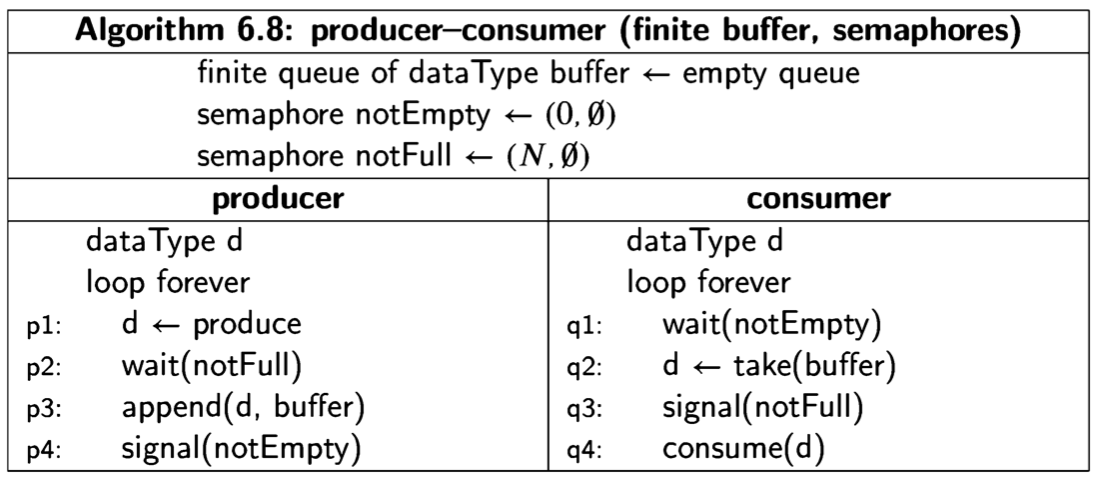
Split semaphores

Algorithm 6.8 uses a technique called split semaphores. This is not a new sema- phore type, but simply a term used to describe a synchronization mechanism built from semaphores. A split semaphore is a group of two or more semaphores satis- fying an invariant that the sum of their values is at most equal to a fixed number N. In the case of the bounded buffer, the invariant:

\[ notEmpty + notFull = N \]

holds at the beginning of the loop bodies.

In the case that N = 1, the construct is called a split binary semaphore. Split binary semaphores were used in Algorithm 6.5 for mergesort.

Compare the use of a split semaphore with the use of a semaphore to solve the critical section problem. Mutual exclusion was achieved by performing the wait and signal operations on a semaphore within a single process. In the bounded buffer algorithm, the wait and signal operations on each semaphore are in different processes. Split semaphores enable one process to wait for the completion of an event in another.

Definitions of semaphores

There are several different definitions of the semaphore type and it is important to be able to distinguish between them. The differences have to do with the specification of liveness properties; they do not affect the safety properties that follow from the semaphore invariants, so the solution we gave for the critical-section problem satisfies the mutual exclusion requirement whatever definition we use.

Strong semaphores

The semaphore we defined is called a weak semaphore and can be compared with a strong semaphore. The difference is that S.L, the set of processes blocked on the semaphore S, is replaced by a queue:

Recall (page 114) that we gave a scenario showing that starvation is possible in the solution for the critical section problem with more than two processes. For a strong semaphore, starvation is impossible for any number N of processes. Suppose p is blocked on S, that is, p appears in the queue S.L. There are at most $N - 1$ processes in S.L, so there are at most $N - 2$ processes ahead of p on the queue. After at most $N - 2$ signal(S) operations, p will be at the head of the queue S.L so it will unblocked by the next signal(S) operation.

Busy-wait semaphores

A busy-wait semaphore does not have a component S.L, so we will identify S with S.V. The operations are defined as follows:

Semaphore operations are atomic so there is no interleaving between the two statements implementing the wait(S) operation.

With busy-wait semaphores you cannot ensure that a process enters its critical section even in the two-process solution, as shown by the following scenario:

Line 4 is identical to line 1 so these states can repeat indefinitely. The scenario is fair, in the technical sense of Section 2.7, because process q is selected infinitely often in the interleaving, but because it is always selected when S = 0, it never gets a chance to successfully complete the wait(S) operation.

Busy-wait semaphores are appropriate in a multiprocessor system where the waiting process has its own processor and is not wasting CPU time that could be used for other computation. They would also be appropriate in a system with little contention so that the waiting process would not waste too much CPU time.

Abstract definitions of semaphores

The definitions given above are intended to be behavioral and not to specify data structures for implementation. The set of the weak semaphore is a mathematical entity and is only intended to mean that the unblocked process is chosen arbitrarily. The queue of the strong semaphore is intended to mean that processes are unblocked in the order they were blocked (although it can be difficult to specify what order means in a concurrent system [37]). A busy-wait semaphore simply allows interleaving of other processes between the signal and the unblocking of a blocked process. How these three behaviors are implemented is unimportant.

It is possible to give abstract definitions of strongly fair and weakly fair sema- phores, similar to the definitions of scheduling fairness given in Section 2.7 (see [58, Section 10.1]). However, these definitions are not very useful, and any real implementation will almost certainly provide one of the behaviors we have given.

The problem of the dining philosophers

The problem of the dining philosophers is a classical problem in the field of concurrent programming. It offers an entertaining vehicle for comparing various formalisms for writing and proving concurrent programs, because it is sufficiently simple to be tractable yet subtle enough to be challenging.

The problem is set in a secluded community of five philosophers who engage in only two activities—thinking and eating:

Meals are taken communally at a table set with five plates and five forks (Figure 6.3). In the center of the table is a bowl of spaghetti that is endlessly replenished. Unfortunately, the spaghetti is hopelessly tangled and a philosopher needs two forks in order to eat.” Each philosopher may pick up the forks on his left and right, but only one at a time. The problem is to design pre and post protocols to ensure that a philosopher only eats if she has two forks. The solution should also satisfy the correctness properties that we described in the chapter on mutual exclusion.

The correctness properties are:

A philosopher eats only if she has two forks.
Mutual exclusion: no two philosophers may hold the same fork simultaneously.
Freedom from deadlock.
Freedom from starvation (pun!).
Efficient behavior in the absence of contention.

Here is a first attempt at a solution, where we assume that each philosopher is initialized with its index i, and that addition is implicitly modulo 5.

Each fork is modeled as a semaphore: wait corresponds to taking a fork and signal corresponds to putting down a fork. Clearly, a philosopher holds both forks before eating.

Theorem 6.3 No fork is ever held by two philosophers.

Proof: Let $P_i$ be the number of philosophers holding fork i, so that $P_i = wait(fork[i]) - signal(fork[i])$. By the semaphore invariant (6.2), $fork[i] = 1 + (-P_i)$, or $P_i = 1 - fork[i]$. Since the value of a semaphore is non-negative (6.1), we conclude that $P_i \leq 1 $

Unfortunately, this solution deadlocks under an interleaving that has all philosophers pick up their left forks—execute $wait(fork[i])$ before any of them tries to pick up a right fork. Now they are all waiting on their right forks, but no process will ever execute a signal operation.

One way of ensuring liveness in a solution to the dining philosophers problem is to limit the number of philosophers entering the dining room to four:

The addition of the semaphore room obviously does not affect the correctness of the safety properties we have proved.

Theorem 6.4 The algorithm is free from starvation.

Proof: We must assume that the semaphore room is a blocked-queue semaphore so that any philosopher waiting to enter the room will eventually do so. The fork semaphores need only be blocked-set semaphores since only two philosophers use each one. If philosopher i is starved, she is blocked forever on a semaphore. There are three cases depending on whether she is blocked on $fork[i]$, $fork[i+1]$ or room.

Case 1: Philosopher i is blocked on her left fork. Then philosopher $ i - 1 $ holds $fork[i]$ as her right fork, that is, philosopher $ i - 1 $ has successfully executed both her wait statements and is either eating, or about to signal her left or right fork semaphores. By progress and the fact that there are only two processes executing operations on a fork semaphore, eventually she will release philosopher i.

Case 2: Philosopher $i$ is blocked on her right fork. This means that philosopher $ i + 1 $ has successfully taken her left fork $(fork[i+1])$ and will never release it. By progress of eating and signaling, philosopher $ i + 1 $ must be blocked forever on her right fork. By induction, it follows that if i is blocked on her right fork, then so must all the other philosophers: $ i + j, 1 < j < 4 $. However, by the semaphore invariant on room, for some $i$, philosopher $i + j$ is not in the room, thus obviously not blocked on a fork semaphore.

Case 3: We assume that the room semaphore is a blocked-queue semaphore, so philosopher i can be blocked on room only if its value is zero indefinitely. By the semaphore invariant, there are at most four philosophers executing the statements between wait(room) and signal(room). The previous cases showed that these philosophers are never blocked indefinitely, so one of them will eventually execute signal(room). I

Another solution that is free from starvation is an asymmetric algorithm, which has the first four philosophers execute the original solution, but the fifth philosopher waits first for the right fork and then for the left fork:

Again it is obvious that the correctness properties on eating are satisfied. Proofs of freedom from deadlock and freedom from starvation are similar to those of the previous algorithm and are left as an exercise.

A solution to the dining philosophers problem by Lehmann and Rabin uses random numbers. Each philosopher “flips a coin” to decide whether to take her left or right fork first. It can be shown that with probability one no philosopher starves [48, Section 11.4].

Barz’s simulation of general semaphores

In this section we present Hans W. Barz’s simulation of a general semaphore by a pair of binary semaphores and an integer variable [6]. (See [67] for a survey of the attempts to solve this problem.) The simulation will be presented within the

context of a solution of the critical section problem that allows $k > 0$ processes simultaneously in the critical section (Algorithm 6.13).

k is the initial value of the general semaphore, statements $p1..6$ simulate the wait statement, and statements $p7..11$ simulate the signal statement. The binary semaphore gate is used to block and unblock processes, while the variable count holds the value of the integer component of the simulated general semaphore. The second binary semaphore S is used to ensure mutual exclusion when accessing count. Since we will be proving only the safety property that mutual exclusion holds, it will be convenient to consider the binary semaphores as busy-wait semaphores, and to write the value of the integer component of the semaphore gate as gate, rather than gate.V.

It is clear from the structure of the algorithm that S is a binary semaphore; it is less clear that gate is one. Therefore, we will not assume anything about the value of gate other than that it is an integer and prove (Lemma 6.5(6), below) that it only takes on the values 0 and 1.

Let us start with an informal description of the algorithm. Since gate is initial- ized to 1, the first process attempting to execute a simulated wait statement will succeed in passing pl: wait(gate), but additional processes will block. The first process and each subsequent process, up to a total of $k - 1$, will execute p5: sig- nal(gate), releasing additional processes to successfully complete p1: wait(gate). The if statement at p4 prevents the kth process from executing p5: signal(gate), so further processes will be blocked at p1: wait(gate).

When $count = 0$, a single simulated signal operation will increment count and exe- cute p11: signal(gate), unblocking one of the processes blocked at p1: wait(gate); this process will promptly decrement count back to zero. A sequence of simulated signal operations, however, will cause count to have a positive value, although the value of gate remains | since it is only signaled once. Once count has a positive value, one or more processes can now successfully execute the simulated wait.

An inductive proof of the algorithm is quite complex, but it is worth studying be- cause so many incorrect algorithms have been proposed for this problem.

In the proof, we will reduce the number of steps in the induction to three. The binary semaphore S prevents the statements $p2..6$ from interleaving with the state- ments $p7..11$. pl can interleave with statements $p2..6$ or $p7..11$, but cannot affect their execution, so the effect is the same as if all the statements $p2..6$ or $p7..11$ were executed before p1.?

We will use the notation entering for $p2..6$ and in CS for p7. We also denote by #entering, respectively #inCS, the number of processes for which entering, respectively in CS, is true.

Lemma 6.5 The conjunction of the following formulas is invariant:

$entering \rightarrow (gate = 0)$
$entering \rightarrow (count > 0)$
$entering \leq 1$
$((gate = 0) \land \neg entering) \rightarrow (count = 0)$
$(count \leq 0) \rightarrow (gate = 0)$
$(gate = 0) \lor (gate = 1)$

Proof: The phrase by (n), A holds will mean: by the inductive hypothesis on formula (n), A must be true before executing this statement. The presentation is somewhat terse, so before reading further, make sure that you understand how material implications can be falsified (Appendix B.3).

Initially:

All processes start at pl, so the antecedent is false.
As for (1).
$entering = 0$.
$gate = 1$ so the antecedent is false.
$count = k > 0$ so the antecedent is false.
$gate = 1$ so the formula is true.

Executing p1:

By (6), $gate < 1$, so p1: wait(gate) can successfully execute only if $gate = 1$, making the consequent $gate = 0$ true.
entering becomes true, so the formula can be falsified only if the consequent is false because $count < 0$. But pl does not change the value of count, so we must assume $count < 0$ before executing the statement. By (5), $gate = 0$, so the p1: wait(gate) cannot be executed.
This can be falsified only if entering is true before executing pl. By (1), if entering is true, then $gate = 0$, so the p1: wait(gate) cannot be executed.
entering becomes true, so the antecedent - entering becomes false.
As for (1).
As for (1).

Executing p2..6:

Some process must be at p2 to execute this statement, so entering is true, and by (3), $entering = 1$. Therefore, the antecedent entering becomes false.
As for (1).
As for (1).
By (1), $gate = 0$, and by (2), $count > 0$. If $count = 1$, the consequent $count = 0$ becomes true. If $count > 1$, p3, p4 and p5 will be executed, so that gate becomes 1, falsifying the antecedent.
By (1), $gate = 0$, and by (2), $count > 0$. If $count > 1$, after decrementing its value in p3, $count > 0$ will become true, falsifying the antecedent. If $count = 1$, the antecedent becomes true, but p5 will not be executed, so $gate = 0$ remains true.
By (1), $gate = 0$ and it can be incremented only once, by p5.

Executing p7..11:

The value of entering does not change. If it was true, by (2) $count > 0$, so that count becomes greater than 1 by p8, ensuring by the if statement at p9 that the value of gate does not change in p10.
The value of entering does not change, and the value of count can only increase.
Trivially, the value of #entering is not changed.
Suppose that the consequent $count = 0$ were true before executing the statements and that it becomes false. By the if statement at p9, statement p10: signal(gate) is executed, so the antecedent $gate = 0$ is also falsified. Suppose now that both the antecedent and the consequent were false; then the antecedent cannot become true, because the value of entering does not change, and if $gate = 0$ is false, it certainly cannot become true by executing p10: signal(gate).
The consequent can be falsified only if $gate = 0$ were true before executing the statements and p10 was executed. By the if statement at p9, that can happen only if $count = 0$. Then $count = 1$ after executing the statements, falsifying the antecedent. If the antecedent were false so that $count > 0$, it certainly remains false after incrementing count in p8.
The formula can be falsified only if $gate = 1$ before executing the statements and p10: signal(gate) is executed. But that happens only if $count = 0$, which implies $gate = 0$ by (5).

Lemma 6.6 The formula $count = k - inCS$ is invariant.

Proof: The formula is initially true by the initialization of count and the fact that all processes are initially at their non-critical sections. Executing pl does not change any term in the formula. Executing $p2..6$ increments #inCS and decrements count, preserving the invariant, as does executing $p7..11$, which decrements #inCS and increments count.

Theorem 6.7 Mutual exclusion holds for Algorithm 6.13, that is, $inCS < k$ is invariant.

Proof: Initially, $inCS < k$ is true since $k > 0$. The only step that can falsify the formula is $p2..6$ executed in a state in which $inCS = k$. By Lemma 6.6, in this state $count = 0$, but entering is also true in that state, contradicting (2) of Lemma 6.5. I

Udding’s starvation-free algorithm

There are solutions to the critical-section problem using weak semaphores that are free of starvation. We give without proof a solution developed by Jan T. Udding [68]. Algorithm 6.14 is similar to the fast algorithms described in Section 5.4, with two gates that must be passed in order to enter the critical section.

The two semaphores constitute a split binary semaphore satisfying $0 < gate1 + gate2 < 1$, and the integer variables count the number of processes about to enter or trying to enter each gate.

The semaphore gatel is reused to provided mutual exclusion during the initial increment of numGate1. In our model, where each line is an atomic operation, this protection is not needed, but freedom from starvation depends on it so we have included it.

The idea behind the algorithm is that processes successfully pass through a gate (complete the wait operation) as a group, without interleaving wait operations from the other processes. Thus a process p passing through gate2 into the critical section may quickly rejoin the group of processes in front of gate1, but all of the colleagues from its group will enter the critical section before p passes the first gate again. This ensures that the algorithm is free from starvation.

The attempted solution still suffers from the possibility of starvation, as shown by the following outline of a scenario:

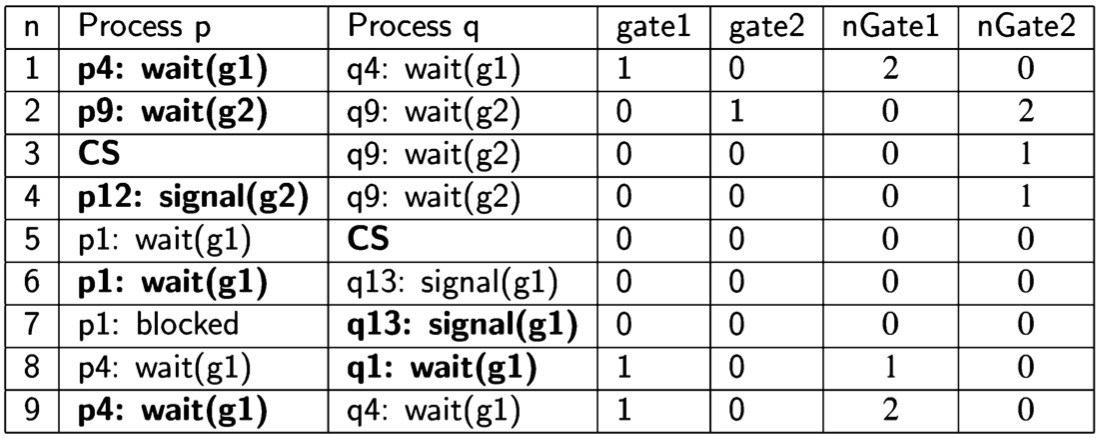
Two processes are denoted p and q with appropriate line numbers; the third process r is omitted because it remains blocked at rl: wait(g1) throughout the scenario. Variable names have been shortened: gate to g and numGate to nGate.

The scenario starts with processes p and q at gates p4 and q4, respectively, while the third process r has yet to pass the initial wait operation at r1. The key line in the scenario is line 7, where q unblocks his old colleague p waiting again at p1 instead of r who has been waiting at r1 for quite a long time.

By adding an additional semaphore, we can ensure that at most one process is at the second gate at any one time. The semaphore onlyOne is initialized to 1, a wait(onlyOne) operation is added before p4 and a signal(onlyOne) operation is added before p9. This ensures that at most one process will be blocked at gate1.

Semaphores in Java

The Semaphore class is defined within the package java.util.concurrent. The terminology is slightly different from the one we have been using. The integer component of an object of class Semaphore is called the number of permits of the object, and unusually, it can be initialized to be negative. The wait and signal operations are called acquire and release, respectively. The acquire operation can throw the exception InterruptedException which must be caught or thrown.

Here is a Java program for the counting algorithm with a semaphore added to ensure that the two assignment statements are executed with no interleaving.

import java.util.concurrent.Semaphore;

class CountSem extends Thread {
  static volatile int n = 0;
  static Semaphore s = new Semaphore(1);

  @override
  public void run() {
    int temp;
    for (int i = 0; i < 10; ++i) {
      try {
        s.acquire();
      } catch (InterruptedException e) {}
      temp = n;
      n = temp + 1;
      s.release();
    }
  }
}

The constructor for class Semaphore includes an extra boolean parameter used to specify if the semaphore is fair or not. A fair semaphore is what we have called a strong semaphore, but an unfair semaphore is more like a busy-wait semaphore than a weak semaphore, because the release method simply unblocks a process but does not acquire the lock associated with the semaphore. (See Section 7.11 for more details on synchronization in Java.)

Monitors

The semaphore was introduced to provide a synchronization primitive that does not require busy waiting. Using semaphores we have given solutions to common concurrent programming problems. However, the semaphore is a low-level primitive because it is unstructured. If we were to build a large system using semaphores alone, the responsibility for the correct use of the semaphores would be diffused among all the implementers of the system. If one of them forgets to call signal(S) after a critical section, the program can deadlock and the cause of the failure will be difficult to isolate.

Monitors provide a structured concurrent programming primitive that concentrates the responsibility for correctness into modules. Monitors are a generalization of the kernel or supervisor found in operating systems, where critical sections such as the allocation of memory are centralized in a privileged program. Applications programs request services which are performed by the kernel. Kernels are run in a hardware mode that ensures that they cannot be interfered with by applications programs.

The monitors discussed in this chapter are decentralized versions of the monolithic kernel. Rather than have one system program handle all requests for services involving shared devices or data, we define a separate monitor for each object or related group of objects that requires synchronization. If operations of the same monitor are called by more than one process, the implementation ensures that these are executed under mutual exclusion. If operations of different monitors are called, their executions can be interleaved.

Monitors have become an extremely important synchronization mechanism because they are a natural generalization of the object of object-oriented programming, which encapsulates data and operation declarations within a class. At runtime, objects of this class can be allocated, and the operations of the class invoked on the fields of the object. The monitor adds the requirement that only one pro- cess can execute an operation on an object at any one time. Furthermore, while the fields of an object may be declared either public (directly accessible outside the class) or private (accessible only by operations declared within the class), the fields of a monitor are all private. Together with the requirement that only one process at a time can execute an operation, this ensures that the fields of a monitor are accessed consistently.

Actual implementations of monitors in programming languages and systems are quite different from one another. We begin the chapter by describing the classical monitor, a version of which is implemented in the BACI concurrency simulator. Then we will discuss protected objects of Ada, followed by synchronized methods in Java which can be used to implement monitors. It is extremely important that you learn how to analyze different implementations: their advantages, their disadvantages and the programming paradigms appropriate to each one.

TL;DR

Monitor-like constructs are the most popular form of synchronization found in programming languages. These constructs are structured and integrate well with the techniques of object-oriented programming. The original formulation by Hoare and Brinch Hansen has served as inspiration for similar constructs, in particular the synchronized methods of Java, and the very elegant protected objects of Ada. As with semaphores, it is important to understand the precise semantics of the construct that you are using, because the style of programming as well as the correctness and efficiency of the resulting programs depend on the details of the implementation.

Both the semaphore and the monitor are highly centralized constructs, blocking and unblocking processes, maintaining queues of blocked processes and encapsulating data. As multiprocessing and distributed architectures become more popular, there is a need for synchronization constructs that are less centralized. These constructs are based upon communications rather than upon sharing. The next chapter presents several models that achieve synchronization by using communications between sending processes and receiving processes.

Declaring and using monitors

In Section 2.5, we discussed the importance of atomic statements. Even the trivial Algorithm 2.4 showed that interleaving a pair of statements executed by each of two processes could lead to unexpected scenarios. The following algorithm shows the same two statements encapsulated within a monitor:

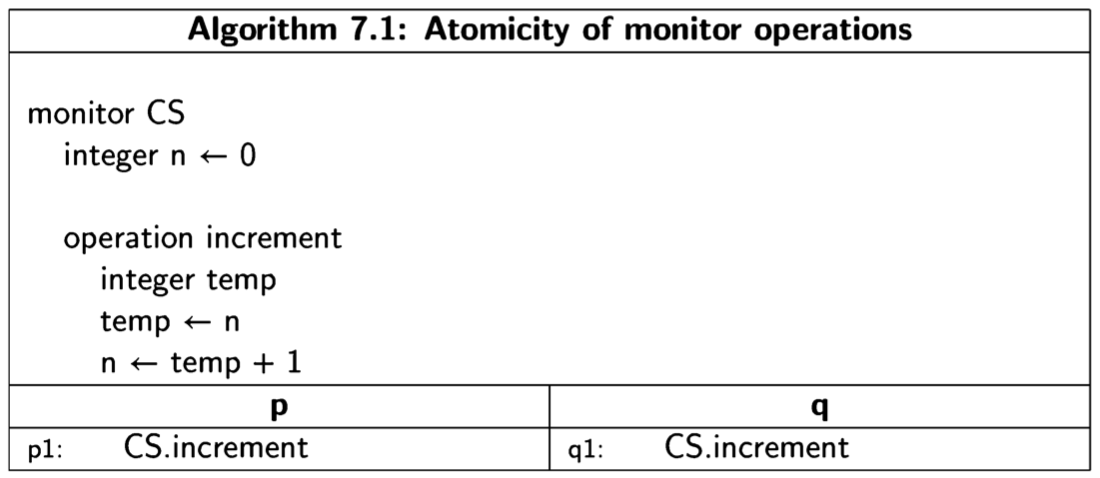
The monitor CS contains one variable n and one operation increment; two statements are contained within this operation, together with the declaration of the local variable. The variable n is not accessible outside the monitor. Two processes, p and q, each call the monitor operation CS.increment. Since by definition only one process at a time can execute a monitor operation, we are ensured mutual exclusion in access to the variable, so the only possible result of executing this algorithm is that n receives the value 2. The following diagram shows how one process is executing statements of a monitor operation while other processes wait outside:

This algorithm also solves the critical section problem, as can be seen by substituting an arbitrary critical section statement for the assignment statements. Compare this solution with the solution to the critical section problem using semaphores given in Section 6.3. The statements of the critical section are encapsulated in the monitor rather than replicated in each process. The synchronization is implicit and does not require the programmers to correctly place wait and signal statements.

The monitor is a static entity, not a dynamic process. It is just a set of operations that sit there waiting for a process to invoke one of them. There is an implicit lock on the door to the monitor, ensuring only one process is inside the monitor at any time. A process must open the lock to enter the monitor; the lock is then closed and remains closed until the process leaves the monitor.

As with semaphores, if there are several processes attempting to enter a monitor, only one of them will succeed. There is no explicit queue associated with the monitor entry, so Starvation is possible.

In our examples, we will declare single monitors, but in real programming languages, a monitor would be declared as a type or a class and you can allocate as many objects of the type as you need.

Condition variables

A monitor implicitly enforces mutual exclusion to its variables, but many problems in concurrent programming have explicit synchronization requirements. For example, in the solution of the producer-consumer problem with a bounded buffer (Section 6.7), the producer must be blocked if the buffer is full and the consumer must be blocked if the buffer is empty. There are two approaches to providing synchronization in monitors. In one approach, the required condition is named by an explicit condition variable (sometimes called an event). Ordinary boolean expressions are used to test the condition, blocking on the condition variable if necessary; a Separate statement is used to unblock a process when the condition becomes true. The alternate approach is to block directly on the expression and let the implementation implicitly unblock a process when the expression is true. The classical monitor uses the first approach, while the second approach is used by protected objects (Section 7.10). Condition variables are one of the synchronization constructs in pthreads, although they are not part of an encapsulating structure like monitors.

Simulating semaphores

Let us see how condition variables work by simulating a solution to the critical section problem using semaphores:

We refrain from giving line numbers for the statements in the monitor because each operation is executed as a single atomic operation.

The monitor implementation follows directly from the definition of semaphores. The integer component of the semaphore is stored in the variable s and the condition variable cond implements the queue of blocked processes. By convention, condition variables are named with the condition you want to be true. waitC(notZero) is read as wait for notZero to be true, and signalC(notZero) is read as signal that notZero is true. The names waitC and signalC are intended to reduce the possibility of confusion with the similarly-named semaphore statements.

If the value of s is zero, the process executing Sem.wait—the simulated semaphore operation—executes the monitor statement waitC(notZero). The process is said to be blocked on the condition:

A process executing waitC blocks unconditionally, because we assume that the condition has been tested for in a preceding if statement; since the entire monitor operation is atomic, the value of the condition cannot change between testing its value and executing waitC. When a process executes a Sem.signal operation, it unblocks the first process (if any) blocked on that condition.

Operations on condition variables

With each condition variable is associated a FIFO queue of blocked processes. Here is the definition of the execution of the atomic operations on condition variables by an arbitrary process p:

Process p is blocked on the queue cond. Process p leaves the monitor, releasing the lock that ensures mutual exclusion in accessing the monitor.

If the queue cond is nonempty, the process at the head of the queue is unblocked. There is also an operation that checks if the queue is empty:

Since the state of the process executing the monitor operation waitC becomes blocked, it is clear that it must release the lock to enable another process to enter the monitor (and eventually signal the condition). In the case of the signalC operation, the unblocked process becomes ready and there is no obvious requirement for the signaling operation to leave the monitor (see Section 7.5).

The following table summarizes the differences between the monitor operations and the similarly-named semaphore operations:

Semaphore	Monitor
wait may or may not block	waitC always blocks
signal always has an effect	signalC has no effect if queue is empty
signal unblocks an arbitrary blocked process	signalC unblocks the process at the head of the queue
a process unblocked by signal can resume execution immediately	a process unblocked by signalC must wait for the signaling process to leave monitor

Correctness of the semaphore simulation

When constructing a state diagram for a program with monitors, all the statements of a monitor operation can be considered to be a single step because they are executed under mutual exclusion and no interleaving is possible between the statements. In Algorithm 7.2, each state has four components: the control pointers of the two processes p and q, the value of the monitor variable s and the queue associated with the condition variable notZero. Here is the state diagram assuming that the value of s has been initialized to 1:

Consider, first, the transition from the state (p2: Sem.signal, ql: Sem.wait, 0, <>) at the top center of the diagram to the state (p2: Sem.signal, blocked, 0, < q >) at the upper right. Process q executes the Sem.wait operation, finds that the value of s is 0 and executes the waitC operation; it is then blocked on the queue for the condition variable notZero.

Consider, now, the transition from (p2: Sem.signal, blocked, 0, < g >) to the state (p1: Sem.wait, q2: Sem.signal, 0, <>) at the lower left of the diagram. Process p executes the Sem.signal operation, incrementing s, and then signalC will unblock process q. As we shall discuss in Section 7.5, process q immediately resumes the execution of its Sem.wait operation, so this can be considered as part of the same atomic statement. q will decrement s back to zero and exit the monitor. Since signalC(nonZero) is the last statement of the Sem.signal operation executed by process p, we may also consider that that process exits the monitor as part of the atomic statement. We end up in a state where process q is in its critical section, denoted in the abbreviated algorithm by the control pointer indicating the next invocation of Sem.signal, while process p is outside its critical section, with its control pointer indicating the next invocation of Sem.wait.

There is no state of the form (p2: Sem.signal, q2: Sem.signal, ..., ...) in the diagram, so the mutual exclusion requirement is satisfied.

The state diagram for a monitor can be relatively simple, because the internal transitions of the monitor statements can be grouped into a single transition.

The producer-consumer problem

Algorithm 7.3 is a solution for the producer-consumer problem with a finite buffer using a monitor. Two condition variables are used and the conditions are explicitly checked to see if a process needs to be suspended. The entire processing of the buffer is encapsulated within the monitor and the buffer data structure is not visible to the producer and consumer processes.

The immediate resumption requirement

The definition of signalC(cond) requires that it unblock the first process blocked on the queue for cond. When this occurs, the signaling process (say p) can now continue to execute the next statement after signalC(cond), while the unblocked process (say q) can execute the next statement after the waitC(cond) that caused it to block. But this is not a valid state, since the specification of a monitor requires that at most one process at a time can be executing statements of a monitor operation. Either p or q will have to be blocked until the other completes its monitor operation. That is, we have to specify if signaling processes are given precedence over waiting processes, or vice versa, or perhaps the selection of the next process is arbitrary. There may also be processes blocked on the entry to the monitor, and the specification of precedence has to take them into account.

Note that the terminology is rather confusing, because the waiting processes are processes that have just been released from being blocked, rather than processes that are waiting because they are blocked.

The following diagram shows the states that processes can be in: waiting to enter the monitor, executing within the monitor (but only one), blocked on condition queues, on a queue of processes just released from waiting on a condition, and on a queue of processes that have just completed a signal operation:

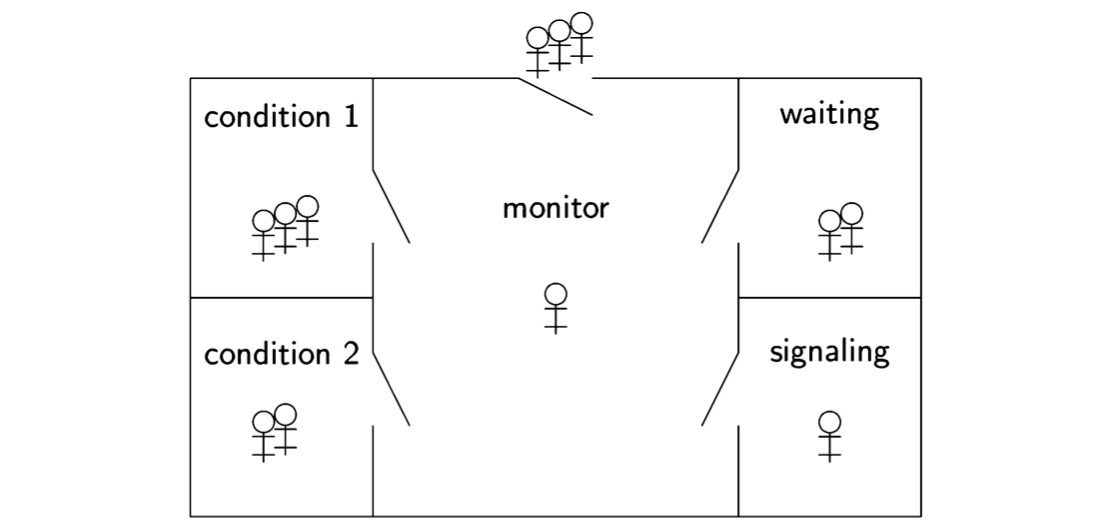
Let us denote the precedence of the signaling processes by S, that of the waiting processes by W and that of the processes blocked on the entry by E. There are thirteen different ways of assigning precedence, but many of them make no sense. For example, it does not make sense to have E greater than either W or S', because that would quickly cause starvation as new processes enter the monitor before earlier ones have left. The classical monitor specifies that $E < S < W$ and later we will discuss the specification E = W < S that is implemented in Java. See [15] for an analysis of monitor definitions.

The specification $E < S < W$ is called the immediate resumption requirement (IRR), or signal and urgent wait. It means that when a process blocked on a condition variable is signaled, it immediately begins executing ahead of the signaling process. It is easy to see the rationale behind IRR. Presumably, the signaling process has changed the state of the monitor (modified its variables) so that the condition now holds; if the waiting process resumes immediately, it can assume the condition does hold and continue with the statements in its operation. For example, look again at the monitor that simulates a semaphore (Algorithm 7.2). The Sem.signal operation increments s just before executing the signalC(notZero) statement; if the Sem.wait operation resumes immediately, it will find s to be nonzero, the condition it was waiting for.

Similarly, in Algorithm 7.3, the monitor solution for the producer-consumer problem, append(v, Buffer) immediately precedes signalC(notEmpty), ensuring that the buffer is not empty when a consumer process is unblocked, and the statement w < head(Buffer) immediately precedes signalC(notFull), ensuring that the buffer is not full when a producer process is unblocked. With immediate resumption there is no need to recheck the status of the buffer.

Without the IRR, it would be possible for the signaling process to continue its execution, causing the condition to again become false. Waiting processes would have to recheck the boolean expression for the condition in a while loop:

The disadvantage of the IRR is that the signaling process might be unnecessarily delayed, resulting in less concurrency than would otherwise be possible. However, if—as in our examples—signalC(cond) is the last statement in a monitor operation, there is no need to block the execution of the process that invoked the operation.

The problem of the readers and writers

The problem of the readers and writers is similar to the mutual exclusion problem in that several processes are competing for access to a critical section. In this problem, however, we divide the processes into two classes:

Readers Processes which are required to exclude writers but not other readers.

Writers Processes which are required to exclude both readers and other writers.

The problem is an abstraction of access to databases, where there is no danger in having several processes read data concurrently, but writing or modifying data must be done under mutual exclusion to ensure consistency of the data. The concept database must be understood in the widest possible sense; even a couple of memory words in a real-time system can be considered a database that needs mutual exclusion when being written to, while several processes can read it simultaneously.

Algorithm 7.4 is a solution to the problem using monitors. We will use the term reader for any process executing the statements of reader and writer for any process executing the statements of writer.

The monitor uses four variables:

readers The number of readers currently reading the database after successfully executing StartRead but before executing EndRead.

writers The number of writers currently writing to the database after successfully executing StartWrite but before executing EndWrite.

OKtoRead A condition variable for blocking readers until it is OK to read. OKtoWrite A condition variable for blocking writers until it is OK to write.

The general form of the monitor code is not difficult to follow. The variables readers and writers are incremented in the Start operations and decremented in the End operations to reflect the natural invariants expressed in the definitions above. At the beginning of the Start operations, a boolean expression is checked to see if the process should be blocked, and at the end of the End operations, another boolean expression is checked to see if some condition should be signaled to unblock a process.

A reader is suspended if some process is currently writing (writers 4 0) or if some process is waiting to write (-empty(OKtoWrite)). The first condition is obviously required by the specification of the problem. The second condition is a decision to give the first blocked writer precedence over waiting readers. A writer is blocked only if there are processes currently reading (readers # 0) or writing (writers 4 0). StartWrite does not check the condition queues.

EndRead executes signalC(OKtoWrite) if there are no more readers. If there are blocked writers, one will be unblocked and allowed to complete StartWrite. EndWrite gives precedence to the first blocked reader, if any; otherwise it unblocks a blocked writer, if any.

Finally, what is the function of signalC(OKtoRead) in the operation StartRead? This statement performs a cascaded unblocking of the blocked readers. Upon termination of a writer, the algorithm gives precedence to unblocking a blocked reader over a blocked writer. However, if one reader is allowed to commence reading, we might as well unblock them all. When the first reader completes StartRead, it will signal the next reader and so on, until this cascade of signals unblocks all the blocked readers.

What about readers that attempt to start reading during the cascaded unblocking? Will they have precedence over blocked writers? By the immediate resumption requirement, the cascaded unblocking will run to completion before any new reader is allowed to commence execution of a monitor operation. When the last signalC(OKtoRead) is executed (and does nothing because the condition queue is empty), the monitor will be released and a new reader may enter. However, it is subject to the check in StartRead that will cause it to block if there are waiting writers.

These rules ensure that there is no starvation of either readers or writers. If there are blocked writers, a new reader is required to wait until the termination of (at least) the first write. If there are blocked readers, they will (all) be unblocked before the next write.

Correctness of the readers and writers algorithm

Proving monitors can be relatively succinct, because monitor invariants are only required to hold outside the monitor procedures themselves. Furthermore, the immediate resumption requirement allows us to infer that what was true before executing a Signal is true when a process blocked on that condition becomes unblocked.

Let R be the number of readers currently reading and W the number of writers currently writing. The proof of the following lemma is immediate from the structure of the program.

Lemma 7.1 The following formulas are invariant:

\[ R > 0 \] \[ W > 0 \] \[ R = readers \] \[ W = writers \]

We implicitly use these invariants to identify changes in the values of the program variables readers and writers with changes in the variables R and W that count processes. The safety of the algorithm is expressed using the variables R and W:

Theorem 7.2 The following formula is invariant: \[ ( R > 0 \rightarrow W=0 ) \land ( W \leq 1) \land ( W =1 \rightarrow R = 0)\]

In words, if a reader is reading then no writer is writing; at most one writer is writing; and if a writer is writing then no reader is reading.

Proof: Clearly, the formula is initially true. Because of the properties of the monitor, there are eight atomic statements: execution of the four monitor operations from start to completion, and execution of the four monitor operations that include signalC statements unblocking a waiting process.

Consider first executing a monitor operation from start to completion:

StartRead: This operation increments R and could falsify $ R > 0 \rightarrow W =0$, but the if statement ensures that the operation completes only if $W = 0$ is true. The operation could falsify $R = 0$ and hence $W = 1 \rightarrow R = O$, but again the if statement ensures that the operation completes only if $W = 1$ is false.
EndRead: This operation decrements R, possibly making $R > 0$ false and $R = O$ true, but these changes cannot falsify the invariant.
StartWrite: This operation increments W and could falsify $W < 1$, but the if statement ensures that the operation completes only if $W = 0$ is true. The operation could falsify $W = 0$ and hence $R > 0 \rightarrow W = 0$, but the if statement ensures that $R > 0$ is false.
EndWrite: This operation decrements W,so $W = 0$ and $W < 1$ could both become true while $W = 1$ becomes false; these changes cannot falsify the invariant.

Consider now the monitor operations that result in unblocking a process from the queue of a condition variable.

signal(OKtoRead) in StartRead: The execution of StartRead including signal(OKtoRead) can cause a reader r to become unblocked. But the if statement ensures that this happens only if $W = 0$, and the IRR ensures that r continues its execution immediately so that $W = 0$ remains true.
signal(OKtoRead) in EndWrite: By the inductive hypothesis, $W < 1$, so $W = 0$ when the reader resumes, preserving the truth of the invariant.
signal(OKtoWrite) in EndRead: The signal is executed only if $R = 1$ upon starting the operation; upon completion $R = 0$ becomes true, preserving the truth of the first and third subformulas. In addition, if $R = 1$, by the inductive hypothesis we also have that $W = 0$ was true. By the IRR for StartWrite of the unblocked writer, $W = 1$ becomes true, preserving the truth of the second subformula.
signal(OKtoWrite) in EndWrite: By the inductive hypothesis $W < 1$, the writer executing EndWrite must be the only writer that is writing so that $W = 1$. By the IRR, the unblocked writer will complete StartWrite, preserving the truth of $W = 1$ and hence $W < 1$. The value of R is, of course, not affected, so the truth of the other subformulas is preserved.

The expressions not empty(OKtoWrite) in StartRead and empty(OKtoRead) in EndWrite were not used in the proof because they are not relevant to the safety of the algorithm.

We now prove that readers are not starved and leave the proof that writers are not starved as an exercise. It is important to note that freedom from starvation holds only for processes that start executing StartRead or StartWrite, because starvation is possible at the entrance to a monitor. Furthermore, both reading and writing are assumed to progress like critical sections, so starvation can occur only if a process is blocked indefinitely on a condition variable.

Let us start with a lemma relating the condition variables to the number of processes reading and writing:

Lemma 7.3 The following formulas are invariant:

\[\neg empty(OKtoRead) \rightarrow (W \neq 0) \lor \neg empty(OKtoWrite)\] \[\neg empty(OKtoWrite) \rightarrow (R \neq 0) \lor (W \neq 0).\]

Proof: Clearly, both formulas are true initially since condition variables are initialized as empty queues.

The antecedent of the first formula can only become true by executing StartRead, but the if statement ensures that the consequent is also true. Can the consequent of the formula become false while the antecedent is true? One way this can happen is by executing EndWrite for the last writer. By the assumption of the truth of the antecedent = empty(OKtoRead), signalC(OKtoRead) is executed. By the IRR, this leads to a cascade of signals that form part of the atomic monitor operation, and the final signal falsifies $\neg$ empty(OKtoRead). Alternatively, EndRead could be executed for the last reader, causing signalC(OKtoWrite) to falsify a empty(OKtoWrite). But this causes $(W \neq 0)$ to become true, so the consequent remains true.

The truth of the second formula is preserved when executing StartWrite by the condition of the if statement. Can the consequent of the formula become false while the antecedent is true? Executing EndRead for the last reader falsifies $R \neq 0$, but since - empty(OKtoWrite) by assumption, signalC(OKtoWrite) makes $W \neq 0$ true. Executing EndWrite for the last (only) writer could falsify $W \neq 0$, but one of the signalC statements will make either $R \neq 0$ or $W \neq 0$ true.

Theorem 7.4 Algorithm 7.4 is free from starvation of readers.

Proof: Ifa reader is starved is must be blocked indefinitely on OKtoRead. We will show that a signal(OKtoRead) statement must eventually be executed, unblocking the first reader on the queue. Since the condition queues are assumed to be FIFO, it follows by (numerical) induction on the position of a reader in the queue that it will eventually be unblocked and allowed to read.

To show

\[\neg empty(OKtoRead) \rightarrow \diamond signalC(OKtoRead)\]

assume to the contrary that

\[\neg empty(OKtoRead) \land \square \neg signalC(OKtoRead).\]

By the first invariant of Lemma 7.3, $(W \neq 0) \lor \neg empty(OKtoWrite)$. If ( W \neq 0), by progress of the writer, eventually EndWrite is executed; signalC(OKtoRead) will be executed since by assumption $\neg$ empty(OKtoRead) is true (and it remains true until some signalC(OKtoRead) statement is executed), a contradiction.

If $\neg$ empty(OKtoWrite) is true, by the second invariant of Lemma 7.3, $(R \neq 0) \lor (W \neq 0)$. We have just shown that $W \neq 0$ leads to a contradiction, so consider the case that $R \neq 0$. By progress of readers, if no new readers execute StartRead, all readers eventually execute EndReader, and the last one will execute signalC(OKtoWrite); since we assumed that > empty(OKtoWrite) is true, a writer will be unblocked making $W \neq 0$ true, and reducing this case to the previous one. The assumption that no new readers successfully execute StartRead holds because = empty(OKtoWrite) will cause a new reader to be blocked on OKtoRead.

A monitor solution for the dining philosophers

Algorithm 6.10, an attempt at solving the problem of the dining philosophers with semaphores, suffered from deadlock because there is no way to test the value of two fork semaphores simultaneously. With monitors, the test can be encapsulated, so that a philosopher waits until both forks are free before taking them.

Algorithm 7.5 is a solution using a monitor. The monitor maintains an array fork which counts the number of free forks available to each philosopher. The takeForks operation waits on a condition variable until two forks are available. Before leaving the monitor with these two forks, it decrements the number of forks available to its neighbors. After eating, a philosopher calls releaseForks, which, in addition to updating the array fork, checks if freeing these forks makes it possible to signal a neighbor.

Let eating[i] be true if philosopher i is eating, that is, if she has successfully executed takeForks(i)and has not yet executed releaseForks(i). We leave it as an exercise to show that $eating[i] \leftrightarrow (forks[i] = 2)$ is invariant. This formula expresses the requirement that a philosopher eats only if she has two forks.

Theorem 7.5 Algorithm 7.5 is free from deadlock.

Proof: Let E be the number of philosophers who are eating, In the exercises, we ask you to show that the following formulas are invariant:

\[\neg empty(OKtoEat[i]) \rightarrow (fork[i] < 2)\ \ \ \ (7.1)\] \[\sum_{i=0}^{4} fork[i] = 10 - 2 * E\ \ \ \ (7.2)\]

Deadlock implies E = 0 and all philosophers are enqueued on OKtoEat. If no philosophers are eating, from (7.2) we conclude $\sum fork[i] = 10$. If they are all enqueued waiting to eat, from (7.1) we conclude $\sum fork[i] \leq 5$ which contradicts the previous formula.

Starvation is possible in Algorithm 7.5. Two philosophers can conspire to starve their mutual neighbor as shown in the following scenario (with the obvious abbreviations):

Philosophers 1 and 3 both need a fork shared with philosopher 2. In lines 1 and 2, they each take a pair of forks, so philosopher 2 is blocked when trying to take forks in line 3. In lines 4 and 5 philosopher 1 releases her forks and then immediately takes them again; since forks[2] does not receive the value 2, philosopher 2 is not signaled. Similarly, in lines 6 and 7, philosopher 3 releases her forks and then immediately takes them again. Lines 4 through 7 of the scenario can be continued indefinitely, demonstrating starvation of philosopher 2.

Protected objects

In the classical monitor, tests, assignment statements and the associated statements waitC, signalC and emptyC must be explicitly programmed. The protected object simplifies the programming of monitors by encapsulating the manipulation of the queues together with the evaluation of the expressions. This also enables significant optimization of the implementation. Protected objects were defined and implemented in the language Ada, though the basic concepts have been around since the beginning of research on monitors. The construct is so elegant that it is worthwhile studying it in our language-independent notation, even if you don’t use Ada in your programming.

Algorithm 7.6 is a solution to the problem of the readers and writers that uses a protected object. As with monitors, execution of the operations of a protected object is done under mutual exclusion. Within the operations, however, the code consists only of the trivial statements that modify the variables.

Synchronization is performed upon entry to and exit from an operation. An operation may have a suffix when expression, called a barrier. The operation may start executing only when the expression of the barrier is true. If the barrier is false, the process is blocked on a FIFO queue; there is a separate queue associated with each entry. (By a slight abuse of language, we will say that the barrier is evaluated and its value is true or false.) In Algorithm 7.6, StartRead can be executed only if no process is writing and StartWrite can be executed only if no process is either reading or writing.

When can a process become unblocked? Assuming that the barrier refers only to variables of the protected object, their values can be changed only by executing an operation of the protected object. So, when the execution of an operation has been completed, all barriers are re-evaluated; if one of them is now true, the process at

the head of the FIFO queue associated with that barrier is unblocked. Since the process evaluating the barrier is terminating its operation, there is no failure of mutual exclusion when a process is unblocked.

In the terminology of Section 7.5, the precedence specification of protected objects is $E < W$. Signaling is done implicitly upon the completion of a protected action so there are no signaling processes. Servicing entry queues is given precedence over new processes trying to enter the protected objects.

Starvation is possible in Algorithm 7.6; we leave it as an exercise to develop algorithms that are free from starvation.

Protected objects are simpler than monitors because the barriers are used implicitly to carry out what was done explicitly with condition variables. In addition, protected objects enable a more efficient implementation. Consider the following outline of a scenario of Algorithm 7.4, the monitor solution to the readers and writers problem:

When the writer executes signalC(OKtoRead), by the IRR it must be blocked to let a reader process be unblocked. But as soon as the process exits its monitor operation, the blocked signaling process is unblocked, only to exit its monitor operation. These context switches are denoted by the breaks in the table. Even with the optimization of combining signalC with the monitor exit, there will still be a context switch from the signaling process to the waiting process.

Consider now a similar scenario for Algorithm 7.6, the solution that uses a protected object:

The variables of the protected object are accessible only from within the object itself. When the writer resets the variable writing, it is executing under mutual exclusion, so it might as well evaluate the barrier for reader and even execute the statements of reader’s entry! When it is finished, both processes can continue executing other statements. Thus a protected action can include not just the execution of the body of an operation, but also the evaluation of the barriers and the execution of the bodies of other operations. This reduces the number of context switches that must be done; as a context switch is usually much more time-consuming than simple statements, protected objects can be more efficient than monitors.

To enable this optimization, it is forbidden for barriers to depend on parameters of the entries. That way there need be only one queue per entry, not one queue per entry call, and the data needed to evaluate the barrier are globally accessible to all operations, not just locally in the entry itself. In order to block a process on a queue that depends on data in the call, the entry call first uses a barrier that does not depend on this data; then, within the protected operation, the data are checked and the call is requeued on another entry. A discussion of this topic is beyond the scope of this book.

Monitors in Java

In Java, there is no special construct for a monitor; instead, every object has a lock that can be used for synchronizing access to fields of the object. Listing 7.3 shows a class for the producer—consumer problem. Once the class is defined, we can declare objects of this class:

PCMonitor monitor = new PCMonitor();

and then invoke its methods:

monitor.Append(5);
int n = monitor.Take();

The addition of the synchronized specifier to the declaration of a method means that a process must acquire the lock for that object before executing the method. From within a synchronized method, another synchronized method of the same object can be invoked while the process retains the lock. Upon return from the last synchronized method invoked on an object, the lock is released.

There are no fairness specifications in Java, so if there is contention to call synchronized methods of an object an arbitrary process will obtain the lock.

A class all of whose methods are declared synchronized can be called a Java monitor. This is just a convention because—unlike the case with protected objects in Ada there is no syntactical requirement that all of the methods of an object be declared as synchronized. It is up to the programmer to ensure that no synchronization errors occur when calling an unsynchronized method.

A Java monitor for the producer—consumer problem

class PCMonitor {
  final int N = 5;
  int Oldest = 0, Newest = 0;
  volatile int Count = 0;
  int Buffer[] = new int[N];

  synchronized void Append(int V) {
    while (Count == N) {
      try {
        wait();
      } catch (InterruptedException e) {}
    }
    Buffer[Newest] = V;
    Newest = (Newest + 1) % N;
    Count = Count + 1;
    notifyAll();
  }

  synchronized void Take() {
    while (Count == 0) {
      try {
        wait();
      } catch (InterruptedException e) {}
    }
    temp = Buffer[Oldest];
    Oldest = (Oldest + 1) % N;
    Count = Count - 1;
    notifyAll();
    return temp;
  }
}

If a process needs to block itself—for example, to avoid appending to a full buffer or taking from an empty buffer—it can invoke the method wait. (This method throws InterruptedException which must be thrown or caught.) The method notify is similar to the monitor statement signalC and will unblock one process, while notifyAll will unblock all processes blocked on this object.

The following diagram shows the structure of a Java monitor:

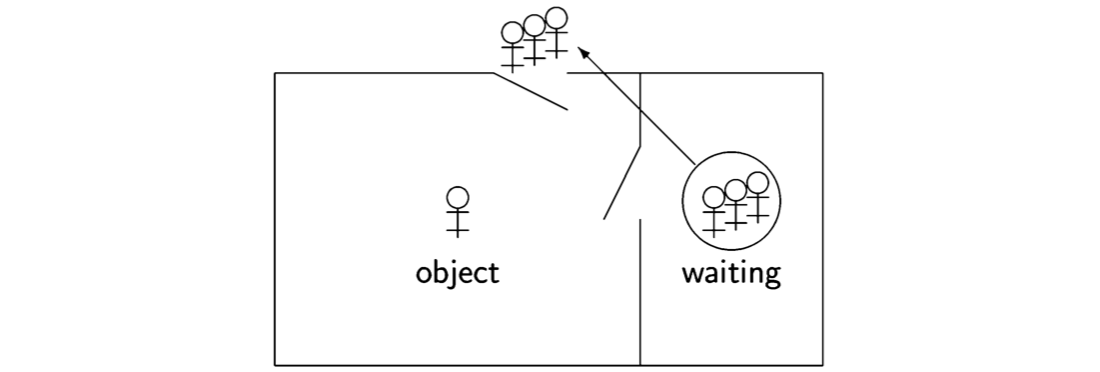
There is a lock which controls the door to the monitor and only one process at a time is allowed to hold the lock and to execute a synchronized method. A process executing wait blocks on this object; the process joins the wait set associated with the object shown on the righthand side of the diagram. When a process joins the wait set, it also releases the lock so that another process can enter the monitor. notify will release one process from the wait set, while notifyAll will release all of them, as symbolized by the circle and arrow.

A process must hold the synchronization lock in order to execute either notify or notifyAll, and it continues to hold the lock until it exits the method or blocks on a wait. The unblocked process or processes must reacquire the lock (only one at a time, of course) in order to execute, whereas with the IRR in the classical monitor, the lock is passed from the signaling process to the unblocked process. Furthermore, the unblocked processes receive no precedence over other processes trying to acquire the lock. In the terminology of Section 7.5, the precedence specification of Java monitors is $ E = W < S $.

An unblocked process cannot assume that the condition it is waiting for is true, so it must recheck it in a while loop before continuing:

synchronized method1() {
  while (!booleanExpression) {
    wait();
  }

  // Assume booleanExpression is true
}

synchronized method2() {
  // Make booleanExpression true
  notifyAll()
}

If the expression in the loop is false, the process joins the wait set until it is unblocked. When it acquires the lock again it will recheck the expression; if it is true, it remains true because the process holds the lock of the monitor and no other process can falsify it. On the other hand, if the expression is again false, the process will rejoin the wait set.

When notify is invoked an arbitrary process may be unblocked so starvation is possible in a Java monitor. Starvation-free algorithms may be written using the concurrency constructs defined in the library java.util.concurrent.

A Java monitor has no condition variables or entries, so that it is impossible to wait on a specific condition. Suppose that there are two processes waiting for conditions to become true, and suppose that process p has called method1 and process q has called method2, and that both have invoked wait after testing for a condition. We want to be able to unblock the process whose condition is now true:

synchronized method1() {
  if (x == 0) {
    wait();
  }
}

synchronized method2() {
  if (y == 0) {
    wait();
  }
}

synchronized method3(...) {
  if ( ... ) {
    x = 10;
    notify (someProcessBlockedInMethod1); // Not legal !!
  } else {
    y = 20;
    notify (someProcessBlockedInMethod2); // Not legal !!
  }
}

Since an arbitrary process will be unblocked, this use of notify is not correct, because it could unblock the wrong process. Instead, we have to use notifyAll which unblocks all processes; these processes now compete to enter the monitor again. A process must wait within a loop to check if its condition is now true:

synchronized method1() {
  while (x == 0) {
    wait();
  }
}

synchronized method2() {
  while (y == 0) {
    wait();
  }
}

synchronized method3(...) {
  if ( ... ) {
    x = 10;
    notify (someProcessBlockedInMethod1); // Not legal !!
  } else {
    y = 20;
    notify (someProcessBlockedInMethod2); // Not legal !!
  }
}

If the wrong process is unblocked it will return itself to the wait set.

However, if only one process is waiting for a lock, or if all the processes waiting are waiting for the same condition, then notify can be used, at a significant saving in context switching.

A Java solution for the problem of the readers and writers is shown in Listing 7.4. The program contains no provision for preventing starvation.

Synchronized blocks

We have shown a programming style using synchronized methods to build monitors in Java. But synchronized is more versatile because it can be applied to any object and to any sequence of statements, not just to a method. For example, we can obtain the equivalent of a critical section protected by a binary semaphore simply by declaring an empty object and then synchronizing on its lock. Given the declaration:

Object obj = new Object();

the statements within any synchronized block on this object in any process are executed under mutual exclusion:

synchronized (obj) {
  // critical section
}

There is no guarantee of liveness, however, because in the presence of contention for a specific lock, an arbitrary process succeeds in acquiring the lock.

A Java monitor for the problem of the readers and the writers

class RWMonitor {
  volatile int readers = 0;
  volatile boolean writing = false;

  synchronized void StartRead() {
    while (writing) {
      try {
        wait();
      } catch (InterruptedException e) {}
    }
    readers = readers + 1;
    notifyAll();
  }

  synchronized void EndRead() {
    readers = readers - 1;
    if (readers == 0) {
      notifyAll();
    }
  }

  synchronized void StartWrite() {
    while (writing || (readers != 0)) {
       try {
        wait();
      } catch (InterruptedException e) {}
      writing = true;
    }
  }

  synchronized void EndWrite() {
    writing = false;
    notifyAll();
  }

Channels

The concurrent programming constructs that we have studied use shared memory, whether directly or through a shared service of an operating system. Now we turn to constructs that are based upon communications, in which processes send and receive messages to and from each other. We will study synchronization in progressively looser modes of communications: in this chapter, we discuss synchronization mechanisms appropriate for tightly coupled systems (channels, rendezvous and remote procedure call); then we discuss spaces which provide communications with persistence; and finally we will study algorithms that were developed for fully distributed systems. As always, we will be dealing with an abstraction and not with the underlying implementation. The interleaving model will continue to be used; absolute time will not be considered, only the relative order in which messages are sent and received by a process.

The chapter begins with an analysis of alternatives in the design of constructs for synchronization by communications. Sections 8.2-8.4 present algorithms using channels, the main topic of the chapter. The implementation of channels in Promela is discussed in Section 8.5. The rendezvous construct and its implementation in Ada is presented in Section 8.6. The final section gives a brief survey of remote procedure calls.

TL;DR

Channels enable us to construct decentralized concurrent programs that do not necessarily share the same address space. Synchronous communication, where the sender and receiver wait for each other, is the basic form of synchronization, as it does not require design decisions about buffering. More complex forms of communication, the rendezvous in Ada and the remote procedure call implemented in many systems, are used for higher-level synchronization, and are especially suited to client-server architectures.

What is common to all the synchronization constructs studied so far is that they envision a set of processes executing more or less simultaneously, so it makes sense to talk about one process blocking while waiting for the execution of a statement in another process. The Linda model for concurrency discussed in the next chapter enables highly flexible programs to be written by replacing process-based synchronization with data-based synchronization.

Models for communications

Synchronous vs. asynchronous communications

Communications by its nature requires two processes—one to send a message and one to receive it—so we must specify the degree of cooperation required between the two processes. In synchronous communications, the exchange of a message is an atomic action requiring the participation of both the sending process, called the sender, and the receiving process, called the receiver. If the sender is ready to send but the receiver is not ready to receive, the sender is blocked, and similarly, if the receiver is ready to receive before the sender is ready to send, the receiver is blocked. The act of communications synchronizes the execution sequences of the two processes. Alternatively, the sender can be allowed to send a message and continue without blocking. Communications are then asynchronous because there is no temporal dependence between the execution sequences of the two processes. The receiver could be executing any statement when a message is sent, and only later check the communications channel for messages.

Deciding on a scheme is based upon the capacity of the communications channel to buffer messages, and on the need for synchronization. In asynchronous communications, the sender may send many messages without the receiver removing them from the channel, so the channel must be able to buffer a potentially unlimited number of messages. Since any buffer is finite, eventually the sender will be blocked or messages will be discarded. Synchronous and asynchronous communications are familiar from telephone calls and email messages. A telephone call synchronizes the activities of the caller and the person who answers. If the persons cannot synchronize, busy signals and unanswered calls result. On the other hand, any number of messages may be sent by email, and the receiver may choose to check the incoming mail at any time. Of course, the capacity of an electronic mailbox is limited, and email is useless if you need immediate synchronization between the sender and the receiver.

The choice between synchronous and asynchronous communications also depends on the level of the implementation. Asynchronous communications requires a buffer for messages sent but not received, and this memory must be allocated somewhere, as must the code for managing the buffers. Therefore, asynchronous communications is usually implemented in software, rather than in hardware. Synchronous communications requires no support other than send and receive instructions that can be implemented in hardware (see Section 8.3).

Addressing

In order to originate a telephone call, the caller must know the telephone number, the address, of the receiver of the call. Addressing is asymmetric, because the receiver does not know the telephone number of the caller. (Caller identification is possible, though the caller may choose to block this option.) Email messages use symmetric addressing, because every message contains the address of the sender.

Symmetric addressing is preferred when the processes are cooperating on the solution of a problem, because the addresses can be fixed at compile time or during a configuration stage, leading to easier programming and more efficient execution. This type of addressing can also be implemented by the use of channels: rather than naming the processes, named channels are declared for use by a pair or a group of processes.

Asymmetric addressing is preferred for programming client-server systems. The client has to know the name of the service it requests, while the server can be programmed without knowledge of its future clients. If needed, the client identification must be passed dynamically as part of the message.

Finally, it is possible to pass messages without any addressing whatsoever! Matching on the message structure is used in place of addresses. In Chapter 9, we will study spaces in which senders broadcast messages with no address; the messages can be received by any process, even by processes that were not in existence when the message was sent.

Data flow

A single act of communications can have data flowing in one direction or two. An email message causes data to flow in one direction only, so a reply requires a separate act of communications. A telephone call allows two-way communications.

Asynchronous communications necessarily uses one-way data flow: the sender sends the message and then continues without waiting for the receiver to accept the message. In synchronous communications, either one- or two-way data flow is possible. Passing a message on a one-way channel is extremely efficient, because the sender need not be blocked while the receiver processes the message. However, if the message does in fact need a reply, it may be more efficient to block the sender, rather than release it and later go through the overhead of synchronizing the two processes for the reply message.

CSP and occam

Channels were introduced by C.A.R. Hoare in the CSP formalism [32], which has been extremely influential in the development of concurrent programming [55, 58]. The programming language occam is directly based upon CSP, as is much of the Promela language that we use in this book. For more information on CSP, occam and their software tools for programming and verification, see the websites listed in Appendix E.

Channels

A channel connects a sending process with a receiving process. Channels are typed, meaning that you must declare the type of the messages that can be sent on the channel. In this section, we discuss synchronous channels. The following algorithm shows how a producer and a consumer can be synchronized using a channel:

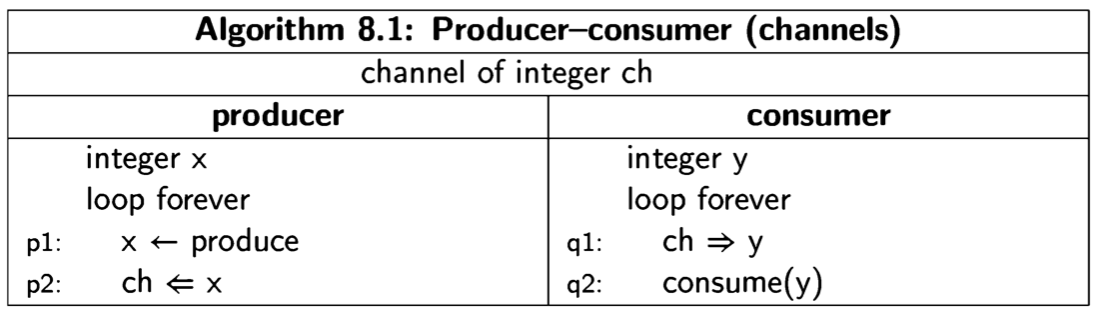
The notation $ch \Leftarrow x$ means that the value of x is sent on the channel ch, and similarly, $ch\Rightarrow y$ means that the value of the message received from the channel is assigned to the variable y. The producer will attempt to send a message at p2, while the consumer will attempt to receive a message at ql. The data transfer will take place only after the control pointers of the two processes reach those points. Synchronous execution of the send and receive operations is considered to be a single change in state. So if $x = v$ in process p, then executing $ch \Leftarrow x$ in p and (ch \Rightarrow y )in process q leads to a state in which $y = v$. Channels in operating systems are called pipes; they enable programs to be constructed by connecting an existing set of programs.

Pipelined computation using channels can be demonstrated using a variant of Conway's problem (Algorithm 8.2). The input to the algorithm is a sequence of characters sent by an environment process to an input channel; the output is the same sequence sent to an environment process on another channel after performing two transformations: (a) runs of $2 \leq n \leq 9$ occurrences of the same character are replaced by the digit corresponding to n and the character; (b) a newline character is appended following every K th character of the transformed sequence.

The algorithm is quite easy to follow because the two transformations are implemented in separate processes: the compress process replaces runs as required and sends the characters one by one on the pipe channel, while the output process takes care of inserting the newline characters:

Channels are efficient and easy to use but they lack flexibility. In particular, it is difficult to program a server using channels, because it is not possible for a server simply to export the interface of the services that it is offering; it must also export a specific set of channels. In other words, programs that use channels must be configured, either at compile time or when the program is initiated. In Section 8.6, we describe the rendezvous which is more flexible and appropriate for writing servers.

Parallel matrix multiplication

One-way channels are extremely efficient, and can be implemented in hardware. There used to be a computing element called a transputer, which contained a CPU, memory and four pairs of one-way channels on a single chip. Synchronous communications was implemented through channel statements which could be directly compiled to machine-language instructions of the transputer. This facilitated the construction of arrays of processors that could be programmed to execute truly parallel programs. While the transputer no longer exists, its architecture has influenced that of modern chips, especially digital signal processors. Here we will demonstrate an algorithm that can be efficiently implemented on such systems.

Consider the problem of matrix multiplication:

Each element of the resulting matrix can be computed independently of the other elements. For example, the element 30 in the bottom right corner of the matrix is obtained by the following computation, which can be performed before, after or simultaneously with the computation of other elements:

We will implement matrix multiplication for 3 x 3 matrices using small numbers, although this algorithm is practical only for large matrices of large values, because of the overhead involved in the communications.

Figure 8.1 shows 21 processors connected so as to compute the matrix multiplication. Each processor will execute a single process. The one-way channels are denoted by arrows. We will use geographical directions to denote the various neighbors of each processor.

The central array of 3 x 3 processes multiplies pairs of elements and computes the partial sums. One process is assigned to each element of the first matrix and initialized with the value of that element. The Source processes are initialized with the row vectors of the second matrix and the elements are sent one by one to the Multiplier processes to the south; they in turn pass on the elements until they are finally caught in the Sink processes. (The Sink processes exist so that the programming of all the Multiplier processes can be uniform without a special case for the bottom row of the array.) A Multiplier process receives a partial sum from the east, and adds to it the result of multiplying its element and the value received from the north. The partial sums are initialized by the Zero processes and they are finally sent to the Result processes on the west.

Let us study the computation of one element of the result:

Process array of matrix multiplication

This is the computation of the corner element that we showed above as a mathematical equation. Since each process waits for its two input values before computing an output, we can read the diagram from right to left: first,$9-0+0=0$, where the partial sum of 0 comes from the Zero process; then, $8-2+0=16$, but now the the partial sum of 0 comes from the Multiplier process labeled 9; finally, using this partial sum of 16, we get $7-2+16=30$ which is passed to the Result process.

Except for the Multiplier processes, the algorithms for the other processes are trivial. A Zero process executes $West \Leftarrow 0$ three times to initialize the Sum variables of a Multiplier process; a Source process executes $South\Leftarrow Vector[i]$ for each of the three elements of the rows of the second matrix; a Sink process executes

$North \Rightarrow dummy$ three times and ignores the values received; a Result process ex- ecutes (East \Rightarrow result) three times and prints or otherwise uses the values received. A Result process knows which row and column the result belongs to: the row is determined by its position in the structure and the column by the order in which the values are received.

Here is the algorithm for a Multiplier process:

Each process must be initialized with five parameters: the element FirstElement and channels that are appropriate for its position in the structure. This configuration can be quite language-specific and we do not consider it further here.

Selective input

In all our examples so far, an input statement ch=>var is for a single channel, and the statement blocks until a process executes an output statement on the corresponding channel. Languages with synchronous communication like CSP, Promela and Ada allow selective input, in which a process can attempt to communicate with more than one channel at the same time:

either
  chl => varl
  or
  ch2 => var2
  or
  ch3 => var3

Exactly one alternative of a selective input statement can succeed. When the statement is executed, if communications can take place on one or more channels, one of them is selected nondeterministically. Otherwise, the process blocks until the communications can succeed on one of the alternatives.

The matrix multiplication program can use selective input to take advantage of additional parallelism in the algorithm. Instead of waiting for input first from North and then from East, we can wait for the first available input and then wait for the other one:

Once one alternative has been selected, the rest of the statements in the alternative are executed normally, in this case, an input statement from the other channel. The use of selective input ensures that the processor to the east of this Multiplier is not blocked unnecessarily.

The dining philosophers with channels

A natural solution for the dining philosophers problem is obtained by letting each fork be a process that is connected by a channel to the philosophers on its left and right. There will be five philosopher processes and five fork processes, shown in the left and right columns of Algorithm 8.5, respectively. The philosopher processes start off by waiting for input on the two adjacent forks channels. Eventually, the fork processes will output values on their channels. The values are of no interest, so we use boolean values and just ignore them upon input. Note that once a fork process has output a value it is blocked until it receives input from the channel. This will only occur when the philosopher process that previously received a value on the channel returns a value after eating.

This works in Promela because a channel can be used by more than one pair of processes.

Rendezvous

The name rendezvous invokes the image of two people who choose a place to meet; the first one to arrive must wait for the arrival of the second. In the metaphor, the two people are symmetric and the rendezvous place is neutral and passive. However, in the synchronization construct, the location of the rendezvous belongs to one of the processes, called the accepting process. The other process, the calling process, must know the identity of the accepting process and the identity of the rendezvous which is called an entry (the same term used in protected objects; see Section 7.10). The accepting process does not know and does not need to know the identity of the calling process, so the rendezvous is appropriate for implementing servers that export their services to all potential clients.

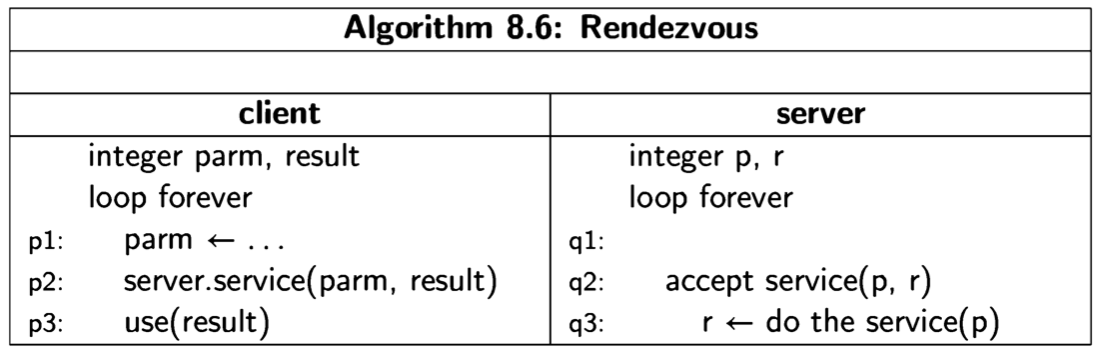
Algorithm 8.6 shows how a rendezvous is used to implement a client-server application. The client process calls the service entry of the server process supplying some parameters; it must now block until the server process is ready to accept the call. Then the rendezvous is performed using the parameters and possibly producing a result. Upon completion of the rendezvous, the result is returned to the client process. At the completion of the rendezvous, the client process is unblocked and the server process remains, of course, unblocked.

The semantics of a rendezvous are illustrated in the following diagram:

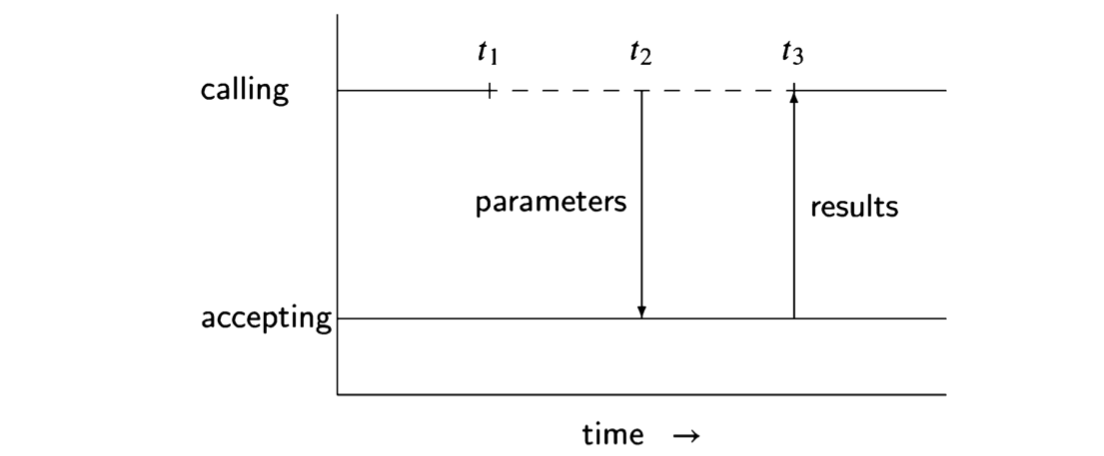
At time $t_1$, the calling process is blocked pending acceptance of the call which occurs at $t_2$. At this time the parameters are transferred to the accepting process. The execution of the statements of the accept block by the accepting process (the interval $t_2–t_3$) is called the execution of the rendezvous. At time $t_3$, the rendezvous is complete, the results are returned to the calling process and both processes may continue executing. We leave it as an exercise to draw the timing diagram for the case where the accepting task tries to execute the accept statement before the calling task has called its entry.

Remote procedure calls

Remote procedure call (RPC) is a construct that enables a client to request a service from a server that may be located on a different processor. The client calls a server in a manner no different from an ordinary procedure call; then, a process is created to handle the invocation. The process may be created on the same processor or on another one, but this is transparent to the client which invokes the procedure and waits for it to return. RPC is different from a rendezvous because the latter involves the active participation of two processes in synchronous communications.

RPC is supported in Ada by the constructs in the Distributed Systems Annex and in Java by the Remote Method Invocation (RMI) library. Alternatively, a system can implement a language-independent specification called Common Object Request Broker Architecture (CORBA). Writing software for distributed systems using RPC is not too difficult, but it is language-specific and quite delicate. We will just give the underlying concepts here and refer you to language textbooks for the details.

To implement RPC, both the client and the server processes must be compiled with a remote interface containing common type and procedure declarations; the client process will invoke the procedures that are implemented in the server process. In Java, a remote interface is created by extending the library interface java. rmi. Remote. In Ada, packages are declared with pragma Remote__Types and pragma Remote__Call__Interface. The following diagram shows what happens when the client calls a procedure that is implemented in the server:

Since the procedure does not actually exist in the client process, the call is processed by a stub. The stub marshals the parameters, that is, it transforms the pa- rameters from their internal format into a sequence of data elements that can be sent through the communications channel. When the remote call is received by the server, it is sent to another stub which unmarshals the parameters, transforming them back into the internal format expected by the language. Then it performs the call to the server program on behalf of the client. If there are return values, similar processing is performed: the values are marshaled, sent back to the client and unmarshaled.

To execute a program using RPC, processes must be assigned to processors, and the clients must be able to locate the services offered by the servers. In Java this is performed by a system called a registry; servers call the registry to bind the services they offer and the clients call the registry to lookup the services they need. In Ada, a configuration tool is used to allocate programs to partitions on the available processors. Again, the details are somewhat complex and we refer you to the language documentation.

Slides

Tema 1: Principios generales de la Concurrencia

Definición

Se da cuando cuando dos o más procesos existen simultáneamente. Distinguir entre existencia y ejecución simultánea (paralelismo).

Un proceso es un programa en ejecución. Formado por:

El código que ejecuta el procesador.
El estado, valores de los registros de la CPU.
La pila de llamadas.
La memoria de trabajo.
Información de la planificación.

Una hebra/hilo es una secuencia de instrucciones dentro de un proceso, que ejecuta sus instrucciones de forma independiente.

Un proceso puede tener varias hebras.

Estas hebras NO comparten:

La pila (cada una posee la suya).
El contador de programa.

SI comparten:

Memoria de procesos (datos).
Recursos del sistema.

Concurrencia vs. Paralelismo

La concurrencia es más general que el paralelismo. Las soluciones que la P.Concurrente da para la sincronización y comunicación son válidas para programas paralelos con memoria común.

Se tiene paralelismo cuando se produce la ejecución simultánea de dos procesos concurrentes.

Algoritmos paralelos.
Métodos de programación paralela.
Procesamiento paralelo.
Arquitectura paralela (procesador multinúcleo).

La concurrencia se encuentra presente en el hardware, en el SO y el software, y en la modelación de casos reales mediante programas.

Sistema concurrente

Sistema informático donde la concurrencia juega un papel importante.

Distinguir entre sistemas inherentemente(deben ser concurrentes si o si) concurrente y potencialmente(pueden ser concurrentes).

Programación concurrente

Conjunto de notaciones y técnicas utilizadas para describir mediante programas el paralelismo potencial de los problemas, resolviendo los problemas de sincronización y comunicación que pueden plantearse.

Características

Mejora de rendimiento
Indeterminación, un programa secuencial es determinista y sigue un orden total. Frente a un programa concurrente, que no es determinista , siguiendo un orden parcial. No significa que el programa sea incorrecto.
No atomicidad.
Velocidad de ejecución de procesos desconocida.
Incertidumbre sobre el resultado.
Entrelazado, un programa concurrente puede tener varias secuencias de ejecución diferentes. Puede haber entrelazados patológicos que lleven a interbloqueos.
Mayor dificultad de verificación de programas.

Speedup

En paralelismo, podemos definir el concepto de speedup como el coeficiente entre el tiempo necesario para completar una tarea secuencialmente y el tiempo necesario para hacerlo en paralelo. (Diferencia entre tiempos ya sea concurrente o paralelo).

$S=\frac{tiempo\ en\ secuencial}{tiempo\ en\ paralelo}$

Clasificación del speedup

Si $S < 1$, la paralelización ha hecho que la solución empeore. En este caso mejor no paralelizar.
Si $1 < S \leq número\ de\ nucleos$, hemos conseguido mejorar la solución en el rango normal. En tareas puramente de cómputo (coef. de bloqueo muy cercano al 0), S debe estar muy próximo al número de nucleos.
Si $S > número\ de\ nucleos$, hemos conseguido una mejor hiperlineal. Son casos poco comunes y solo se dan para determinados problemas en determinadas arquitecturas de memoria caché.

Condiciones de Bernstein

Permiten determinar si dos conjuntos de instrucciones se pueden ejecutar de forma concurrente.

$L(S_k) =$ conjunto de lectura, del conjunto de instrucciones $S_k$.

$E(S_k) =$ conjunto de escritura, del conjunto de instrucciones $S_k$.

Dos conjuntos de instrucciones $S_i$ y $S_j$ se pueden ejecutar de forma concurrente si:

$L(S_i)\cap E(S_j) = \emptyset $
$E(S_i)\cap L(S_j) = \emptyset $
$E(S_i)\cap E(S_j) = \emptyset $

Interbloqueo

Situación en la que todos los procesos quedan a la espera de una situación que nunca se dará.

Hipótesis de progreso finito

No se puede hacer ninguna suposición acerca de las velocidades absolutas o relativas de ejecución de los procesos o hebras, excepto que es mayor que 0
Un programa concurrente se entiende en base a sus componentes (procesos o hebras) y sus interacciones, sin considerar el entorno de ejecución.

Problemas de la concurrencia

Condiciones de concurso

Aparecen cuando varias entidades concurrentes comparten recursos comunes accediendo a ellos simultáneamente. Pueden llevar a problemas graves como sobreescritura de datos, interbloqueos, etc.

Son propias de los sistemas concurrentes. Se caracterizan, a nivel de programación, las zonas de código desde las que las entidades concurrentes acceden a recursos comunes se denominan secciones críticas.

Dado el indeterminismo de los programas concurrentes, la única forma de evitar una condición de concurso será forzar la ejecución aislada de cada sección crítica.

Exclusión mutua

Consiste en evitar la condición de concurso sobre un recurso compartido forzando la ejecución atómica de las secciones críticas de las entidades concurrentes que lo usan. Elimina el entrelazado.

Esto implica detener la ejecución de una entidad concurrente hasta que se produzcan determinadas circustancias: sincronización.

También implica el poder comunicar a otras entidades el estado de una dada: comunicación.

Los lenguajes concurrentes deben permitir ambas.

Beneficios de la exclusión mutua

Dentro de las secciones críticas, no hay entrelazado. Se incrementa el determinismo, ya que se garantiza la ejecución secuencial ("atomicidad"), de las secciones críticas. Permite comunicar a los procesos a través de las secciones críticas. Acota a nivel de código las secciones críticas mediante el uso de protocolos de E/S de las mismas. Pueden generar sobrecargas de ejecución.

Código - precondición - sección crítica - postcondición.

Corrección de Sistemas Concurrentes

Propiedades de corrección

De seguridad:
- Exclusión mutua de las secciones críticas.
- No existen interbloqueos (deadblock).
De vivacidad:
- No existen interbloqueos activos (liveblock).
- No existen inanición de procesos.

Especificación y verificación formal de sistemas concurrentes.

Lógica temporal, CSP (Hoare), redes de Petri.
Metodología gráfica de representación.
Admite modelado dinámico de sistemas concurrentes.
Permite una verificación matemáticamente sencillas de las propiedades de corrección de un sistema concurrente.

Lenguajes concurrentes

Se consideran lenguajes concurrentes a aquellos que permiten expresar la concurrencia directamente, no siendo necesario el recurso el SO o de bibliotecas específicas.

Incluyen herramientas para sincronizar y comunicar a entidades concurrentes. Ej: C++11, Java.

Técnicas de creación de entidades concurrentes

Manuales:

Accediendo directamente al hardware.
Usando bibliotecas software (como herencia de la clase Thread, o implementación de la clase Runnable, Java).

Automáticas:

Bajo la responsabilidad del SO.
Detección del compilador de la concurrencia implícita en un programa secuencial y generación automática de los procesos concurrentes que corresponden.

Modelos de creación de entidades concurrentes

Estático

El número de procesos concurrentes se fijan en tiempo de compilación. No es un método flexible, es seguro, eficaz y limitado.

Dinámico (estándar actual)

Los procesos se crean y destruyen en tiempo de ejecución, es un método flexible, pero menos seguro que el estático. Es usado por los sistemas Unix o Java. Menos estructurado y más dificil de interpretar.

Consideraciones sobre el hardware

Sistemas mono procesador

Son modelos de concurrencia simulado, existe entrelazado entre instrucciones, tiene una arquitectura de memoria común, existe planificación en el acceso al procesador.

Sistemas multiprocesador

Fuerte acoplamiento. (Multiprocesadores)
- Arquitectura de memoria común (UMA)
- Soluciones propuestas para monoprocesadores admisibles
- Existe planificación en el acceso a los núcleos
Acoplamiento débil. (Sistemas distribuidos)
- Arquitectura de comunicaciones
- Memoria no común (NUMA)
- Necesidad de soluciones ad-hoc

Taxonomía de Flynn

SISD
- Ejecución determinista, antiguo modelo de computación
SIMD
- Ejecución determinista y síncrona (con cerrojos). Muy útil en nubes de datos reticulados.
MIMD
- Ejecución determista/no determinista y síncrona/asíncrona. Multiprocesadores, clusters, multicores... Computadoras actuales.

Implementación de programas distribuidos

Modelo de paso de mensajes

Primitivas de comunicación send/receive, carácter de las primitivas, protocolos de solicitud/respuesta de pocas capas.

Modelo RPC/RMI

Permite al programador invocar procedimientos remotos de forma (idealmente) transparente. Requiere procedimientos de resguardos (stubs).

Modelo de Objetos distribuidos

DCOM (Microsoft), CORBA (OMG), EJB (Sun).

Sistemas de tiempo real

Son sistemas concurrentes caracterizados por la existencia de una ligadura temporal para completar la tarea. Control robótico, teledirección, telemedicina, multimedia...

El programador tiene acceso al reloj y al planificador, pueden ser:

Críticos, las tareas deben, necesariamente, satisfacer las restricciones impuestas por la ligadura temporal.
No críticos, las tareas intentan satisfacer tales restricciones, pero el diseño no garantiza la consecución de las mismas con total garantía.

Linux RT y JRTS.

Características: predectibilidad, determinismo, certidumbre, control.

Tema2: Creación y control de `Threads` en Java

Se puede tener de dos formas distintas, o extendiendo de la clase Thread o implementando la interfaz Runnable.

Razones para usar hilos: optimiza el uso de la CPU, se modelan mejor determinados problemas, el problema no admite otra solución razonable.

El método join() o condición de espera, hace que la ejecución espere para continuar hasta que todos los hilos hayan hecho sus tareas.

Las variables que sean static permiten compartir memoria entre los objetos de la clase.

Si hacemos uso de la implementación de la clase Runnable, cualquier clase que lo implemente expresa ejecución concurrente. Y estos objetos se pueden pasar como parámetros al constructor de la clase Thread.

Es posible crear concurrencia mediante expresiones lambda de la siguiente forma:

Runnable r = () -> {};
Thread th = new Thread(r);
th.start();

thread-lifecicle

API de control de thread:

t1.start() → lanza el hilo t1
t1.sleep(int t) → suspende a t1 durante t milisegundos
t1.yield() → pasa a t1 de ejecución a listo
t1.join() → suspende t0 y espera que termine t1

Control de prioridad

La prioridad del hilo hijo será igual a la del hilo padre.

Tiene sentido exclusivamente en el ámbito de la JVM, aunque se mapea a los hilos del sistema.

La clase Thread tiene un esquema de 10 niveles de prioridad.

Ver la prioridad: public int getPriority()
Establecer la prioridad: public void setPriority(int p)

El valor de la prioridad en la JVM indica al planificador del SO qué hilos van primero. Aunque NO es un contrato absoluto, ya que depende de:

La implementación de la JVM
El SO
El mapping de prioridad JVM-prioridad SO

Mapping de hilos

Prioridad Java:

Thread.MIN_PRIORITY; // 1
Thread.NORM_PRIORITY; // 5
Thread.MAX_PRIORITY; // 10

JVM-hilos nativos de Win32

El SO conoce el número de hilos que usa la JVM. Se aplican uno a uno. El secuencionamiento de hilos Java está sujeto al del SO. Se aplican 10 prioridades en la JVM sobre 7 en el SO + 5 prioridades de secuenciamiento.

Thread.MIN_PRIORITY; // THREAD.PRIORITY_LOWEST;
Thread.NORM_PRIORITY; // THREAD.PRIORITY_NORMAL;
Thread.MAX_PRIORITY; // THREAD.PRIORITY_HIGHEST;

JVM-hilos nativos de Linux

Núcleos recientes implementan Native Posix Thread Library. Aplican hilos JVM a hilos del núcleo uno-a-uno bajo el modelo de Solaris. La prioridad Java es un factor muy pequeño en el cálculo global del secuenciamiento.

Thread.MIN_PRIORITY; // 4
Thread.NORM_PRIORITY; // 0
Thread.MAX_PRIORITY; // -5

Conclusiones del control de prioridades

La actual especificación de la JVM no establece un modelo de planificación por prioridades válido. El comportamiento puede y debe variar en diferentes máquinas.

En secuencias de tareas estrictas, no es posible planificar con prioridades. Aunque si con co-rutinas, a nivel básico.

Ejecutores y Pool de Threads

Crear y destruir hilos tiene latencias, esta creación y control son responsabilidad del programador.

Hay determinadas aplicaciones que crean hilos de forma masiva, para las cuales el modelo de threads es ineficiente.

Pool de Threads

Hacen una reserva de hilos a la espera de recibir tareas para ejecutarlas. Solo se crea una vez de manaera que se reduce la latencia y reutiliza los hilos una y otra vez.

Efectúa de forma automática la gestión del ciclo de via de las tareas, recibiendo las tareas a ejecutar mediante objetos Runnable.

ExecutorService singleExecutor = Executors.newSingleThreadExecutor();

ExecutorService fixedExecutor = Executors.newFixedThreadPool(500);

for(...)
    executor.execute(new Thread());

executer.shutdown();
while(!executor.isTerminated());

También tenemos ejecutores que son altamente configurables, que implementan a ExecutorService.

public ThreadPoolExecutor(
    int corePoolSize, int maximumPoolSize, long keepAliveTime,
    TimeUnit unit, BlockingQueue<Runnable> workQueue
);

// Example
ThreadPoolExecutor miPool = new ThreadPoolExecutor(
    tamPool, tamPool, 60000L, TimeUnit.MILLISECONDS,
    new LinkedBlockingQueue<Runnable>()
);

Tarea[] tareas = new Tarea[nTareas];

for(int i=0; i < nTareas; i++){
    tareas[i] = new Tarea(i);
    miPool.execute(tareas[i]);
}

miPool.shutdown();

Ejecución asíncrona a futuro

Interfaz `Callable<V>`

Modela a tareas que admiten ejecución concurrente. Es similar al Runnable, pero no igual. Los objetos que la implementan retorna un resultado de clase V.

Concurrencia soportada por el método V call() que encapsula el código a ejecutar concurrentement, habitualmente procesado a través de un ejecutor. Si el resultado que debe retornar no puede ser computado, lanza una excepción.

Interfaz `Future<V>`

Representa el resultado de una computación asíncrona, tales computación y resultado son provistos por objetos que implementan la interfaz Callable. Es decir, el resultado de una computación asíncrona modelada mediante un objeto que implementa a Callable<V>, se obtiene "dentro" de un Future<V>. Las clases que implementan a Future disponen de métodos para:

Comprobar si la computación a futuro ha sido completada, boolean isDone().
Obtener la computación a futuro cuando ha sido completada, V get().

Este último método es sumamente interesante, provee de sincronización implícita por sí mismo, ya que tiene carácter bloqueante, es decir, se espera con bloqueo hasta que la tarea Callable<V> que tiene que computar el cálculo lo hace y retorna el resultado.

// FactorialTask implements Callable<Integer>, método call() que retorna un Integer
FactorialTask task = new FactorialTask(5);
ExecutorService exec = Executors.newFixedThreadPool(1);
Future <Integer > future = exec.submit(task);
exec.shutdown();
System.out.println(future.get().intValue());

Se puede hacer uso de expresiones lambda para el método V call(). Similar al Runnable, pero retornando un resultado de la clase.

Callable <Integer> computation = () → {
    int fact = 1;
    for(int count = number; count > 1;count--)
        fact = fact * count;
    return (new Integer(fact));
};

Tema 3: Modelos teóricos de control de la concurrencia en sistemas de memoria común

Podemos encontrar varios niveles de abstracción:

Lenguaje: monitores, regiones críticas
Sistema: semáforos
Memoria: espera ocupada

Problema de de la exclusión mutua

Sólo un proceso ejecuta su sección crítica. Para ello, se introducen protocolos de E/S, que suelen requerir variables adicionales.

Un proceso nunca puede pararse en la ejecución de los protocolos o en la sección crítica. No habrá bloqueos, si varios procesos quieren acceder a la sección crítica, alguno lo conseguirá eventualmente.

Tampoco habrá permanencia indefinida de procesos en el pre-protocolo, todos deben tener éxito para entrar en la sección crítica. Es decir no habrá procesos ansiosos.

Igualmente, no hay contenciones, un único proceso deseoso de acceder a la sección crítica lo logrará. Progreso en la ejecución.

Espera ocupada

Se logra la EM mediante protocolos de entrada que consumen ciclos de CPU. Pueden ser:

Soluciones software, las únicas instrucciones atómicas de bajo nivel que consideran son load/store
Algoritmos de Dekker, Peterson, Knuth, Kesell, Eisenberg-MacGuire, Lamport
Soluciones hardware, utilizan instrucciones específicas de lectura-escritura o intercambio de datos en memoria común cuya ejecución es garantizada como de carácter atómico

Soluciones algorítmicas con variables comunes

Vea Turnos.java

Son poco eficientes y muy complejos, en arquitecturas modernas puede funcionar de forma incorrecta y actualmente no se utilizan. Se concretan en los algoritmos de Dekker, Kesell, Peterson, Lamport, Eisenberg-McGuire...

Inconvenientes

Utilizan espera ocupada
Requieren un análisis y programación muy cuidadosos
Están muy ligados a la máquina en la que se implementan
No son transportables
No dan una interfaz directa al programador
Son poco estructurados y difíciles de entender a un número arbitrario de entidades concurrentes

Semáforos

Definición

Es una variable S entera que toma valores no nogativos y sobre la que se pueden realizar dos operaciones. Introducidos por Dijsktra en 1965.

Operaciones soportadas:

Wait(S):
- Si $S>0$, entonces $S = S - 1$
- En otro caso, la entidad concurrente es suspendida sobre $S$, en una cola asociada
Signal(S):
- Si hay una entidad concurrente suspendida, se le despierta
- En otro caso $S = S + 1$

Generalidades

Wait y Signal son operaciones atómicas, el valor inicial es $> 0$, Signal despierta algún proceso, no especificado, habitualmente FIFO.

Hipotesis de corrección

Semáforos generales: $S\ge0$
Semáforos binarios: $S = {0, 1}$

Ecuaciones de invarianza, deben ser satisfechas por cualquier implementación del concepto de semáforo:

$S\ge0$

$S=S_0 + |Signals| - |Waits|$

Nota: |Signals| = número de signals ejecutados, mismo para |Waits|

Implementación

Type semaforo=record of
    S: integer
    L: lista_de_procesos
end

La variable S mantiene el valor actual del semáforo, y L es una estructura de datos, dinámica.

Cuando $S=0$ y un proceso llama a Wait es bloqueado y mantenido en la lista L
Cuando otro proceso señaliza sobre S, alguno de los bloqueados sale de L según algún algoritmo de prioridad

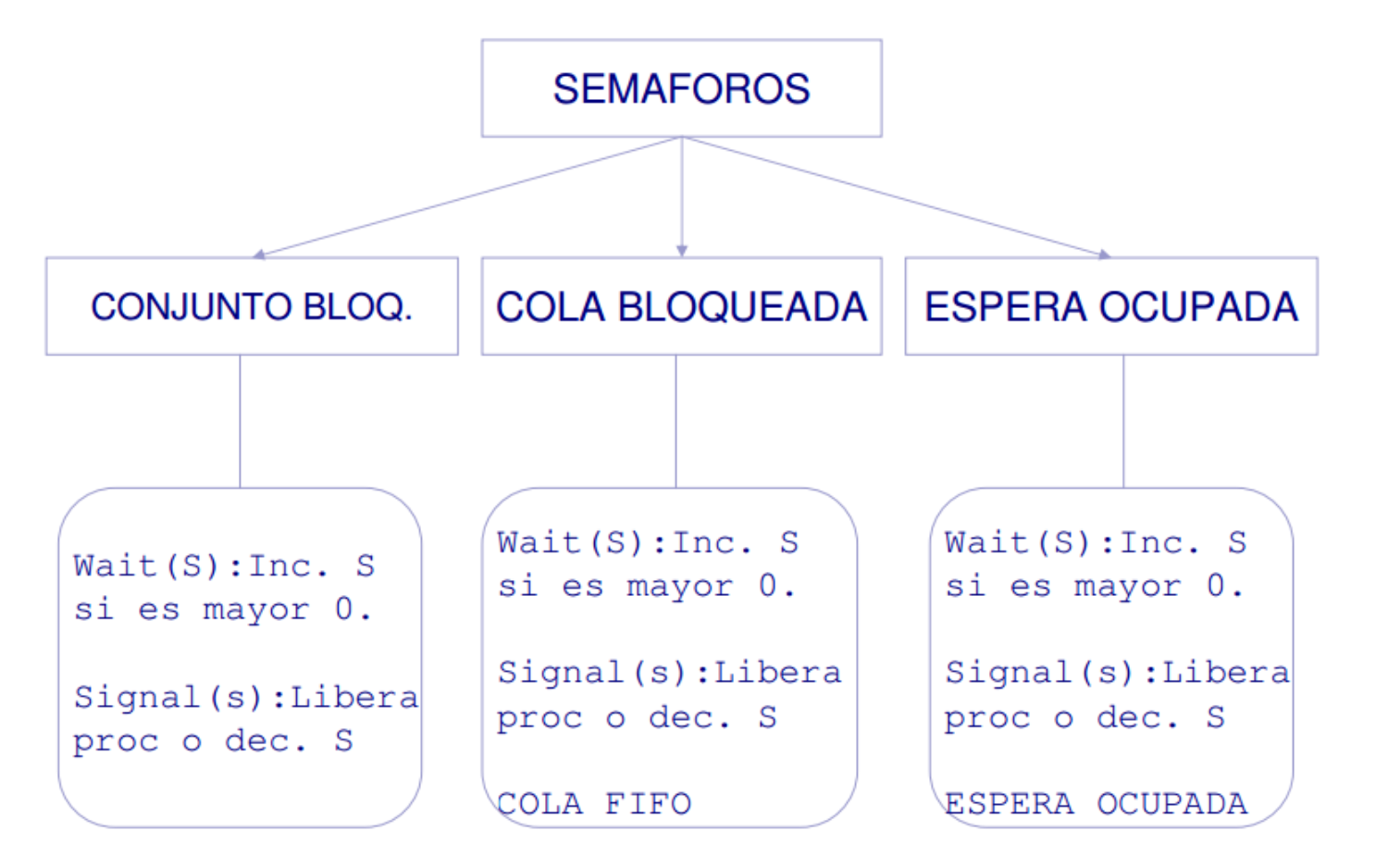
modalidades-semaforos

Semáforos en C

C dispone de una biblioteca sem.h en el marco de facilidades IPC:

Define conjuntos de semáforos
Semántica muy diferente al estándar de Dijkstra
Son mas expresivos
Funciones semget, semctl y semop

Semáforos en Java

No se dispusieron como primitivos hasta 1.5, asi mismo, java proporciona primitivas de control de la exclusión mutua en el acceso concurrente a objetos (cerrojos).

Java permite forzar la ejecución de métodos en exclusión mutua.

private static Semaphore s = new Semaphore(1);
//...
s.acquire(); // wait(S)
s.release(); // signal(S)

Barreras con semáforos

una barrera es un punto del código que ninguna entidad concurrente sobrepasa hasta que todas han llegado a ella.

Inconvenientes de los semáforos

Bajo nivel y no estructurados
Balanceado incorrecto de operaciones
Semántica poco ligada al contexto
Mantenimiento complejo de códigos que hacen uso exhaustivo de semáforos

Sincronización compleja: Productor-Consumidor

Idealmente tenemos un buffer de comunicación infinito.

Productor, pueden insertar tantos datos como desee
Consumidor, solo puede extraer de un buffer con datos presentes

Usamos un semáforo Elements para controlar al consumidor, dos punteros que indican las posiciones donde se extrae o se inserta: In_Ptr, Out_Ptr y acceso a las variables de puntero en EM mediante el uso de un semáforo binario.

productor-consumidor

Regiones críticas

Una región crítica es una sección crítica cuya ejecución bajo EM está garantizada.

Más alto nivel que los semáforos, agrupa acceso a recursos comunes (variables) en regiones (recursos). Variables compartidas etiquetadas como compartidas o recurso.

Un proceso no puede entrar en una región donde ya hay otro, debe esperar. Permiten detectar accesos indebidos en tiempo de compilación.

Semántica

Las entidades concurrentes sólo pueden acceder a variables compartidas dentro de una región crítica, y lo hará en tiempo finito. En tiempo t solo puede haber un proceso dentro de una región crítica.

Una entidad concurrente pasa un tiempo finito dentro de una región crítica, y posteriormente la abandona, un proceso que no pueda entrar en una RC es puesto en espera.

En general, la gestión de la cola de espera es equitativa.

Inconvenientes

Su anidamiento puede producir interbloqueos, no dan soporte para resolver la sincronización.

Mejora: regiones críticas condicionales

Regiones críticas condicionales

Tienen una sintaxis sencilla, aunque una semantica no tanto.

Sintaxis

region identificador when condicion do
    begin
        s1;
        ...;
        sm;
    end

Semántica

rc_condicional

Un proceso que desea ejecutar la región crítica debe conseguir el acceso en EM a la misma. Si ya está ocupada, espera sobre la cola principal.

El proceso que logra la EM a la sección crítica entra en ella y evalúa la condición (1).

Si la condición es cierta, se ejecuta la lista de instrucciones s1,...,sn
Si no, el proceso es enviado (2), a la cola de eventos, en espera a que la condición sea cierta. La exclusión mutua sobre la región crítica se libera

Cuando un proceso termina de ejecutar la sección crítica, la región comprueba si hay procesos en la cola de eventos para los cuáles la re-evaluación de la condición sea cierta.

Si no hay ninguno, la región da paso al proceso que está en el frente de la cola principal
Si hay alguno, se le da acceso a la región

Regiones críticas en C/C++ y Java

En C/C++ no existen como tales, pueden simularse a partir de otras primitivas, como monitores.

En Java, existen mediante bloques synchronized, requieren de un objeto para proveer el bloqueo. El modelo RCC se puede simular mediante un monitor construido con la API de concurrencia estándar.

Monitores

Un monitor es una construcción sintáctica de un lenguaje de programación concurrente que encapsula un recurso crítico a gestionar en exclusión mutua, junto con los procedimientos que lo gestionan. Por tanto se da:

Centralización de recursos
Estructuración de los datos

Características

Encapsulamiento de los datos y alta estructuración
Exclusión mutua de procesos internos por definición
Sincronización mediante el uso del concepto de señal
Compacidad y eficacia
Transparencia al usuario
Tienen las mismas capacidades que los semáfors, son más expresivos

monitores

Estrutura sintáctica

type nombre=monitor
    declaraciones de variables

    procedure entry P1(...)
    begin...end;
    ...
    procedure entry PN(...)
    begin...end;

begin
    codigo de inicialización
end

### Modelo semántico El acceso de las entidades concurrentes al monitor es en exclusión mutua. La variables de condición proveen sincronización.

Una entidad concurrente puede quedar en espera sobre una variable de condición. En ese momento, la exclusión mutua se libera y otras entidades pueden acceder al monitor.

Disciplinas de señalización más usadas:

Señalar y salir, la entidad que señaliza abandona el monitor
Señalar y seguir, la entidad que señaliza sigue en el monitor

### Variables de condición, señales

Permiten sincronizar a las entidades concurrentes que acceden al monitor.

nombre_variable: condition;

Operaciones soportadas:

wait(variable_conditcion), la entidad concurrente que está dentro del monitor y hace la llamada es suspendida en una cola FIFO asociada a la variable en espera de que se cumpla la condición. Exclusión mutua liberada
send(variable_condicion), proceso situado al frente de la cola asociada a la variable despertado
non_empty(variable_condicion), devuelve verdadero si la cola asociada a la variable no está vacía

NOTA: en ocasiones, la sintaxis podrá ser c.wait, c.send para una variable de condición c

Disciplinas de señalización

Tipo	Carácter	Clase de Señal
SA	Señales automáticas	Señales implícitas, incluidas por el compilador. No hay que programar send
SC	Señalar y continuar	Señal explícita no desplazante. El proceso señalador no sale
SX	Señalar y salir	Señal explícita desplazante. El proceso señalador sale. Send debe ser la última instrucción del monitor
SW	Señalar y esperar	Señal explícita desplazante. El proceso señalador sale y es enviado a la cola de entrada del monitor
SU	Señalar con urgencia	Señal explícita desplazante. El proceso señalador sale y es enviado a una cola de procesos urgente, prioritaria en la entrada

Monitores en C/C++ y Java

C++11 proporciona clases que dan soporte a cerrojos y variables de condición. Es posible implantar monitores con un uso combinado.

En java, todo objeto es un monitor potencial.

Clase Object: métodos wait, notify, notifyAll.
Clases con métodos synchronized

Solo soporta variables de condición a partir de Java 1.5, en otro caso, hay que simularlo. Equivalen a una única variable de condición.

Tema 4: Control de la concurrencia en Java (API estándar)

Exclusión mutua entre hilos

En Java, la EM se logra a nivel de objetos. Todo objeto tiene asociado un cerrojo (lock).

Técnicas

Bloques synchronized, el segmento de código que debe ejecutarse en EM se etiqueta asi, es el equivalente a una región crítica en java.
Métodos synchronized, aquellas instancias de recursos que deben manejarse bajo EM se encapsulan en una clase y todos sus métodos modificadores se etiquetan con esta palabra.

Por tanto dos o más hilos están en EM cuando llaman a métodos synchronized de un objeto (de EM) o ejecutan métodos con bloques de código sincronizados.

public metodo_x (parametros) {
    //Resto de codigo del metodo. No se ejecuta en EM.
    /* comienzo de la seccion critica */
    synchronized (object) {
        //Bloque de sentencias criticas
        //Todo el codigo situado entre llaves se ejecuta bajo EM
    }
    /* fin de la seccion critica */
}// metodo_x

Son una implementación del concepto de región crítica. Como cerrojo se puede usar el propio objeto this.

El bloque sólo se ejecuta si se obtiene el cerrojo sobre el objeto. Útil para adecuar código secuencial a un entorno concurrente.

Un método synchronized fuerza la EM entre todos los hilos que lo invocan, tmabién lo hace con otros métodos synchronized del objeto.

Cualquier hilo que trate de ejecutar un método sincronizado deberá esperar si otro método sincronizado ya está en ejecución. Los métodos que no sean sincronizados pueden seguir ejecutándose concurrentemente.

El cerrojo está asociado a cada instancia de una clase, los métodos de clase(static) también pueden ser synchronized.

### Primer protocolo de control de EM

Acceder al recurso compartido donde sea necesario, definir un objeto para control de la exclusión mutua (o usar el this).

Sincronizar el código crítico utilizando el cerrojo del objeto de control dentro de un bloque synchronized de instrucciones.

Segundo protocolo de control de EM

Encapsular el recurso crítico en una clase, definiendo todos los métodos como no estáticos y synchronized. O al menos, todos los modificadores.

Crear hilos que compartan una instancia de la clase creada.

OJO, esto último no provee sincronización.

La posesión del bloqueo es por hilo

Un método sincronizado puede invocar a otro método sincronizado sobre el mismo objeto (REENTRANCIA), permitiendo llamadas recursivas a métodos sincronizados. Permite invocar métodos heredados sincronizados.

Deadlock (Interbloqueo)

Se producen cuando hay condiciones de espera de liberación de bloqueos cruzados entre dos hilos.

Solo pueden evitarse mediante un análisis cuidadoso y riguroso del uso del código sincronizado.

Anidar bloques synchronized produce interbloqueo.

Sincronización entre hilos

En java la sincronización entre hilos se logra con los métodos wait, notify y notifyAll (clase Object). Deben ser utilizados únicamente dentro de métodos o código de tipo synchronized.

Cuando un hilo llama a un método que hace wait las siguientes acciones se ejecutan atómicamente:

Hilo llamante queda suspendido y bloqueado
EM sobre el objeto liberada
Hilo colocado en una cola única (wait-set) de espera asociado al objeto

Cuando un hilo llama a un método que hace notify, uno de los hilos bloqueados en la cola pasa a listo. Java no especifica cual. Depende de la implementación (JVM). Si se llama al método notifyAll, todos los hilos de dicha cola son desbloqueados y pasan a listo. Accederá al objeto aquél que sea planificado.

Si el wait-set está vacío, notify y notifyAll no tienen efecto.

Condiciones de guarda

No se puede escribir código de hilos asumiendo que un hilo concreto recibirá la notificación, diferentes hilos pueden estar bloqueados sobre un mismo objeto a la espera de diferentes condiciones, pero el wait-set es único.

Dado que el notifyAll() los despierta a todos de forma incondicional, es posible que reactive hilos para los cuales no cumplen la condición de espera.

Condición de guarda: siempre que el hilo usuario invoca a wait(), lo primero al despertar es volver a comprobar su condición particular, volviendo al bloqueo si ésta aún no se cumple.

public synchronized void m_receptor_senal() {
    // hilo usuario se bloqueara en el metodo a espera de condicion
    // el hilo usuario pasa al wait-set
    while (!condicion) try {
        wait();
    } // condicion de guarda
    catch ()(Exception e) {}
    //codigo accedido en e.m.
}
public synchronized void m_emisor_senal() {
    /**
    hilo usuario enviara una senal a todos los hilos del waitset
    la guarda garantiza que se despiertan los adecuados
    codigo en e.m. que cambia las condiciones de estado notiyAll();
    */
}

Monitores en `Java`

Un monitor es un objeto que implementa acceso bajo EM a todos sus métodos, y provee sincronización. En Java, son objetos de una clase cuyos métodos públicos son todos synchronized.

Un objeto con métodos synchronized proporciona un cerrojo único que permite implantar monitores con comodidad y EM bajo control.

Los métodos wait, notify y notifyAll permiten sincronizar los accesos al monitor, de acuerdo as la semántica de los mismos ya conocida.

class Monitor {
    //definir aqui datos protegidos por el monitor
    public Monitor() {...} //constructor
    public synchronized tipo1 metodo1() throws InterruptedException {
        ...
        notifyAll();
        ...
        while (!condicion1) wait();
    }

    public synchronized tipo2 metodo2() throws InterruptedException {
        ...
        notifyAll();
        ...
        while (!condicion1) wait();
    }
}

Semántica

Cuando un método synchronized del monitor llama a wait(), libera la EM sobre el monitor y encola al hilo que llamó al método en el wait-set.

Cuando un método synchronized del monitor hace notify(), un hilo del wait-set (no se especifica cual) pasará a la cola de hilos que esperan el cerrojo y se renaudará cuando sea planificado.

Cuando otro método del monitor hace notifyAll(), todos los hilos del wait-set pasarán a la cola de hilos que esperan el cerrojo y se renaudarán cuando sean planificados.

El monitor de Java no tiene variables de condición, sólo una cola de bloqueo de espera implícita.

La política de señalización es señalar y seguir (SC)

El método (hilo) señalador sigue su ejecución
El hilo(s) señalado(s) pasan del wait-set a la cola de procesos que esperan el cerrojo

Para dormir a un hilo a la espera de una condición usamos el método wait(), dentro de un método synchronized. Es menos fino que una variable de condición, y el conjunto de espera es único(wait-set)

### Peculiaridades

No es posible programar a los hilos suponiendo que recibirán la señalización cuándo la necesiten. Al no existir variables de condición, sino una única variable implícita, es conveniente usar notifyAll() para que todos los procesos comprueben la condición que los bloqueó.

No es posible señalar un hilo en concreto, por lo que:

Es aconsejable bloquear a los hilos en el wait-set con una condición de guarda en conjunción con el notifyAll()
while(!condicion) try{wait();} catch (InterruptedException e) {return;}
Todos serán despertados, comprobarán la condición y volverán a bloquearse, excepto los que la encuentren verdadera, que pasan a espera del cerrojo sobre el monitor.

No es aconsejable usar un if en la condición de guarda. Los campos protegidos por el monitor suelen declararse private.

Técnica de diseño en java

Decidir qué datos encapsular en el monitor
Construir un monitor teórico, utilizando tantas variables de condición como sean necesarias
Usar la señalización SC en el monitor teórico
Implementar en Java
1. Escribir un método synchronized por cada procedimiento
2. Hacer los datos encapsulados private
3. Sustituir cada wait(variable_condicion) pos una condición de guarda.
4. Sustituir cada send(variable_condicion) por una llamada a notifyAll()
5. Escribir el código de inicialización del monitor en el constructor del mismo

Ejemplo de monitor

class CubbyHole {
    private int contents;
    private boolean available = false;

    public synchronized int get() {
        while (available == false) {
            try {
                wait();
            } catch (InterruptedException e) {
            }
        }
        available = false;
        notifyAll();
        return contents;
    }

    public synchronized void put(int value) {
        while (available == true) {
            try {
                wait();
            } catch (InterruptedException e) {
            }
        }
        contents = value;
        available = true;
        notifyAll();
    }
}

Control de la concurrencia en Java (API alto nivel)

Disponible a partir de Java 5, mejoras respecto a los mecanismos previos de control de la concurrencia.

Generan menos sobrecarga en tiempo de ejecución
Permiten controlar la e.m. y la sincronización a un nivel más fino
Soporta primitivas clásicas como los semáforos o las variables de condición en monitores
Ofrece cerrojos con mejor soporte a granularidad y al ámbito de uso

API `java.util.concurrent.atomic`

Conjunto de clases que soportan programación concurrente segura sobre variables simples tratadas de forma atómica.

Clases: AtomicBoolean, AtomicInteger, AtomicIntegerArray, AtomicLong, AtomicLongArray, AtomicReference<V>, etc

OJO, no todos los métodos del API de estas clases soportan concurrencia segura. Sólo aquellos en los que se indica que la operación se realiza de forma atómica

La clase `Semaphore`

Permite disponer de semáforos de conteo de semántica mínima o igual a la estándar de Dijkstra, o aumentada.

Métodos principales

Semaphore(long permits)
acquire(), acquire(int permits), equivale a wait
release(), release(long permits), equivale a signal
tryAcquire(), varias versiones
availablePermits()

La clase `CyclicBarrier`

Una barrera es un punto de espera a partir del cuál todos los hilos se sincronizan. Ningún hilo pasará por la barrera hasta que todos los hilos esperados llegan a ella.

Nos pertmite unificar resultados parciales e iniciar la siguiente fase de una ejecución simutánea.

API `java.util.concurrent.locks`

Proporciona clases para establecer sincronización de hilos alternativas a los bloques de código sincronizado y a los monitores.

Clases e interfaces de interés

ReentrantLock, proporciona cerrojos de e.m. de semántica equivalente a synchronized, pero con un manejo más sencillo y una mejor granularidad
LockSupport, proporciona primitivas de bloqueo de hilos que permiten al programador diseñar sus clases de sincronización y cerrojos propios
Condition, es una interfaz cuyas instancias se usan asociadas a locks. Implementan variables de condición y proporcionan una alternativa de sincronización a los métodos wait, notify y notifyAll de la clase Object

API de la clase `ReentrantLock`

Proporciona cerrojos reentrantes de semántica equivalente a synchronized.

Métodos:

lock(), unlock(), isLocked()

Métododo Condition newCondition() retorna una variable de condición asociada al cerrojo.

Interfaz `Condition`

Proporciona variables de condición, se usa asociada a un cerrojo, siendo cerrojo una instancia de la clase ReentrantLock

cerrojo.newCondition() retorna la variable de condición.

Métodos sobre las variables de condición:

await(), signal(), signalAll()

Clases contenedoras sincronizadas

A partir de Java 5 se incorporan versiones sincronizadas de las principales clases contenedoras.

Clases: ConcurrentHashMap, ConcurrentSkipListMap, ConcurrentSkipListSet, CopyOnWriteArrayList y CopyOnWriteArraySet.

Colas sincronizadas

A partir de Java 5 se incorporan diferentes versiones de colas, todas ellas sincronizadas.

Clases: LinkedBlockingQueue, ArrayBlockingQueue, SynchronousQueue, PriorityBlockingQueue y DelayQueue

Características

Son seguras frente a hilos concurrentes, proporcionan notificación a hilos según cambia su contenido.

Son autosincronizadas, proveen sincronización (además de e.m.) por sí mismas.

Facilitan enormemente la programación de patrones de concurrencia como el P-S.

Uso correcto de colecciones

Usamos colecciones a través de interfaces (usabilidad del código)

Colecciones no sincronizadas no mejora mucho el rendimiento, para problemas como productor-consumidor: use colas.

Minimice la sincronización explícita, si con una colección retarda sus algoritmos, distribuya los datos y use varias.

MPJ-Express, modelos teóricos de control de la concurrencia con paso de mensjaes.

Paso de mensajes

Todos los modelos teóricos de control de la concurrencia analizados se basan en la existencia de memoria compartida, a través de la cuál las hebras se comunican a efectos de sincronizar su ejecución.

En sistemas donde esta memoria no existe (sistemas distribuidos, clusters de procesadores), ese conjunto de técnicas no es aplicable. Por lo que necesitamos un nuevo modelo, que estructure la comunicación y sincronización entre hebras mediante el envío de mensajes (a través de algún medio de comunicación).

Ahora las hebras (en general, las tareas) se comunican mediante operaciones de envío y receptión de información de naturaleza explícita.

Arquitectura básica

Se utiliza el concepto de canal como medio común a las tareas que se comunican, el cual es una abstracción software que puede modelar a diferentes realidades físicas, como una red de comunicaciones, internet, o incluso un espacio de memoria común, si este existe y así se decide.

Ahora las tareas envían información al canal (mediante una operación de envío) o la reciben desde el canal (mediante una operación de recepción).

Ventajas

Es aplicable en prácticamente cualquier arquitectura de computadores:

En sistemas distribuidos
En sistemas paralelos con/sin memoria común
En clusters de procesadores

No existe el problema del acceso a datos compartidos y toda la problemática que el mismo conlleva.

Identificación de procesos

Es necesario determinar cómo se identifican entre sí los procesos emisores y receptores de una aplicación:

Denominación directa
- Utilizan directamente los id de los procesos, debiendo asignarse previamente a la ejecución del programa y manteniéndose posteriormente. Si se cambian, hay que recompilar el código de la aplicación
Denominación indirecta
- Utiliza un objeto intermedio denominado buzón, los procesos designan al mismo buzón como destino u origen de los mensjaes que se intercambian

Ejemplos:

// direccionamiento directo
// Proceso P0
int dato;
produce(dato);
send(&dato, P1);

// Proceso P1
int x;
receive(&x, P0);
consume(x);

// direccionamiento indirecto
Channel of Integer Buzon;

//Proceso P0
int dato;
produce(dato);
send(&dato, Buzon);

// Proceso P1
int x;
receive(&x, Buzon);
consume(x);

Semántica de las operaciones

`send` y `receive`

Puede variar, dependerá de la seguridad y el modo de comunicación.

Propiedad de seguridad: una operación send es segura cuando existen garantías de que el valor recibido por el proceso destino es el que tiene los datos justo antes de la llamada en el proceso origen.

Sincronización

Operaciones síncronas, el intercambio de un mensaje es una operación atómica que exige la participación simultánea del emisor y receptor (rendezvouz)
Operaciones asíncronas, el emisor envía el mensaje sin bloquearse, y el emisor lo puede recoger más tarde; requiere de la existencia de un buzón intermedio.

Operaciones síncronas

La comunicación se lleva a cabo mediante un enlace directo entre los procesos implicados.

Las operaciones son bloqueantes, un proceso A no envía si el proceso B de destino no está preparado para recibir. Mientras, A espera.

Un proceso B espera bloqueado para recibir a que haya un proceso A que efectúe un envío.

Por tanto, antes de que los datos se envíen de forma física, ambos procesos han de estar preparados para participar en el intercambio. Debe producirse una cita o rendezvous.

Esto implica:

Sincronización entre emisor y receptor
El emisor puede realizar aserciones acerca del estado del receptor en el punto de sincronización

Operaciones asíncronas

receive posee la misma semántica que el paso de mensajes síncrono. Extraerá los mensajes del buzón intermedio, pero bloqueará al receptor si dicho buzón está vacío.

send posee una semántica diferente, ya que ahora no tiene carácter bloqueante.

El proceso emisor envía, send, su mensaje al buzón, y continúa la ejecución normal. Eventualmente, el envío podría llegar a tener carácter bloqueante si el buzón intermedio llegara a llenarse.

Bibliotecas de paso de mensajes

MPI (C/C++, Fortran, etc.) y sus versiones para Java (MPJ-Express) son muy utilizados para programación paralela con paso de mensajes en arquitecturas multicore de memoria común y clusters de procesadores.
JCSP es una implementación más abstracta y más cercana al concepto de canal expuesto.

La programación en Java con sockets y con el framework RMI ofrece soporte a la programación distribuida basada en el paso de mensajes con un mayor nivel de abstracción.

MPI, message passing interface

Uno de los frameworks más utilizados para programación paralela y distribuida mediante paso de mensajes entre procesos.

Teóricamente soporta el nivel MIMD de la taxonomía de Flynn. Sin embargo, en la práctica, la mayoría de aplicaciones escritas con él utilizan el modelo SPMD, donde todos los procesos ejecutan el mismo programa sobre datos diferentes.

Obviamente, esos programas no necesariamente han de ejecutar la misma instrucción al mismo tiempo.

MPJ-Express, es una implementación de MPI para Java (sobre multicore y clusters)

Funciones

Proporciona funciones de comunicación punto a punto para dos procesos, y funciones colectivas que involucran a un grupo de procesos.

Los procesos pueden agruparse mediante el concepto de comunicador, lo que permite determinar el ámbito de las funciones colectivas y el diseño modular.

MPJ-Expres incluye funciones para realizar operaciones:

Básicas
Comunicación punto a punto
Comunicaciones colectivas
Control de la topología del espacio de procesos
Gestión e interrogatorio del entorno

Funciones básicas

MPI.Init() para iniciar la ejecución paralela
MPI.COMM_WORLD.Size() para determinar el número de procesos en ejecución paralela
MPI.COMM_WORLD.Rank() para que cada proceso obtenga su identificador dentro de la colección de procesos que forman la aplicación
MPI.Finalize() para terminar la ejecución del programa

Comunicadores de MPJ-Express

Un comunicador es un universo de comunicación de MPJ-Express que define a un grupo de procesos que se pueden comunicar entre sí. Todas las funciones de comunicación de MPJ-Express necesitan involucrar a un comunicador.

Todo mensaje de MPJ-Express debe involucrar a un comunicador. El comunicador especificado en las llamadas a operación de envío y recepción debe concordar para que la comunicación sea posible.

Pueden existir múltiples comunicadores y un proceso puede formar parte de varios

Dentro de los comunicadores los procesos se numeran (y se identifican) consecutivamente (empezando por 0). Este es el rank del proceso. Un proceso con varios comunicadores puede tener diferentes rank en cada uno.

MPJ-Express proporciona un comunicador básico por defecto, MPI.COMM_WORLD, que incluye a todos los procesos.

Comunicaciones punto a punto

Hay dos procesos emisor y receptor, deben programarse explícitamente operaciones de envío (en el emisor) y de recepción (en el receptor).

Todo mensaje de MPJ-Express debe involuclar un comunicador, con su id.

Las operaciones más simples del API para enviar y recibir son:

void Send(bufer, offset, datatype, destination, tag)
Status Recv(bufer, offset, datatype, source, tag)

También existe comunicación uno a muchos

Objeto `Status`

El resultado de una operación de recepción es un objeto de clase Status, el cual permite obtener información del mensaje recibido y de su tamaño. Esto se produce cuando los procesos que envían y reciben sincronizan en el mensaje.

Operaciones bloqueantes

Las operaciones Send y Recv descritas son bloqueantes, el proceso que las usa permanece bloqueado hasya que la operación que invocan está completada. Esto se produce cuando los procesos que envían y reciben sincronizan entre sí el mensaje.

Punto a punto síncronas

Las operaciones de envío y recepción realizan un envío sin búfer, bloqueante en los dos extremos que se comunican.

Ahora las operaciones son las siguientes:

void SSend(bufer, offset, datatype, destination, tag)
Status Recv(bufer, offset, datatype, source, tag)

La operación de envío SSend finaliza sólo cuando la operación Recv correspondiente sea invocada por otro proceso y el receptor haya comenzado a recibir el mensaje.

Cuando SSend devuelve el control, la zona de memoria que alberga el dato puede ser reutilizada y el receptor habrá alcanzado el punto de su ejecución que corresponde a la llamada de la función de recepción.

Si la operación de recepción es bloqueante (por ejemplo, Recv) la semántica del paso de mensaje es síncrona (existe cita entre emisor y receptor)

Operaciones de comunicación colectiva

Afectan a todos los procesos de un comunicador concreto. Todos los procesos del comunicador las deben llamar con parámetro iguales. Están definidas en la clase Intracomm

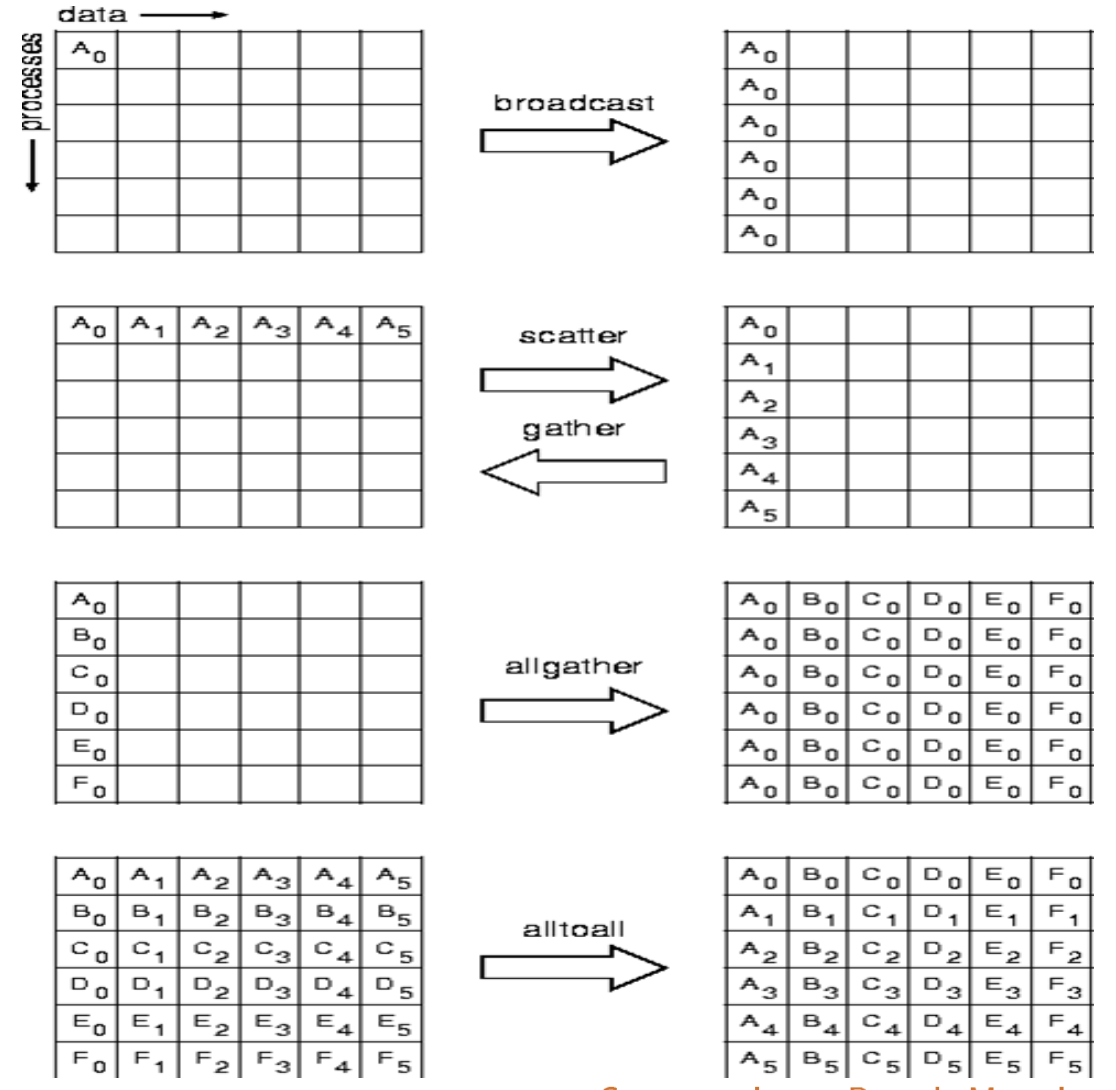
op-com

Paso de mensajes con RMI

Programación distribuida

No existe memoria común, hay comunicaciones, no existe un estado global del sistema, grado de transparencia, escalablas y reconfigurables.

Modelos de programación distribuida

Paso de mensajes (send y receive)
RPC
- Stubs cliente y servidor
- Visión en java es RMI
Objetos distribuidos
- DCOM de Microsoft
- Jini de SUN
- CORBA de OMG

Modelos de paso de mensajes

Mecanismo para comunicar y sincronizar entidades concurrentes que no pueden o no quieren compartir memoria. Se hace uso de llamadas send y receive.

Tipología de llamadas:

BLoqueadas - no bloqueadas
Almacenadas - no almacenadas
Fiables - no fiables

En UNIX, pipes con y sin nombres. En Java:

Sockets, clases Socket y ServerSocket
Canales, CTJ (communicating Threads for Java)

Modelo Romote Procedure Call (RPC)

Mayor nivel de abstracción, llamadas a procedimientos local o remoto indistintamente.

Necesita de stubs/skeletons (ocultamiento), y registro del serviio (servidor de nombres).

En UNIX:

Biblioteca rpc.h
Representación estándar XDR
Automatización parcial, especificación-compilador rpcgen

En java:

Objetos remotos, serialización
Paquete java.rmi
Automatización parcial, interfaz-compilador rmic

Nuestro objetivo será efectuar llamadas como si tuvieran carácter local a un método remoto, enmascarando los aspectos relativos a comunicaciones.

Stubs

Efectúan el marshalling/unmarshalling de parámetros, bloquean al cliente a la espera del resultado. Transparecia de ejecución remota. Interface con el nivel de red (TCP, UDP).

Generación

De forma manual o de forma automática.

Especificación formal de interfaz, software específico, rpcgen (C-UNIX) / rmic (Java).

Nota sobre RPC en C

Especificación de la interfaz del servidor remoto en un fichero de especificación .x

/* rand.x */
program RAND_PROG{
    version RAND_VER{
        void inicia_aleatorio(long)=1;
        double obtener_aleat(void)=2;
    }=1;
    }=0x3111111;

Generación automática de resguardos, rpcgen rand.x

Distribuir y compilar ficheros entre las máquinas implicadas.

Necesario utilizar representación XDR. Biblioteca xdr.h.

RMI en Java

Permite disponer de objetos distribuidos utilizando Java. Un objeto distribuido se ejecuta en una JVM diferente o remota.

Objetivo, lograr una referencia al objeto remoto que permita utilizarlo como si el objeto se estuviera ejecutando sobre la JVM local.

Similar a RPC, si bien el nivel de abstracción es más alto, se puede generalizar a otros lenguajes utilizando JNI. RMI pasa los parámetros y valores de retorno utilizando serialización de objetos.

RPC	RMI
Carácter y estructura de diseño procideimental	Carácter y estructura de diseño orientada a objetos
Es dependiente del lenguaje	Es dependiente del lenguaje
Utiliza la representación externa de datos XDR	Utiliza la serialización de objetos en Java
El uso de punteros requiere el manejo explícito de los mismos	El uso de referencias a objetos locales y remotos es automático
NO hay movilidad de código	El código es móvil, mediante el uso de bytecodes

Llamadas locales vs. llamadas remotas

Un objeto remoto es aquél que se ejecuta en una JVM diferente situada potencialente en un host distinto.

RMI es la acción de invocar a un método de la interfaz de un objeto remoto.

// ejemplo de llamada a metodo local
int dato;
dato = Suma (x,y);

//ejemplo de llamada a metodo remoto (no completo)
IEjemploRMI1 ORemoto =
    (IEjemploRMI1)Naming.lookup("//sargo:2005/EjemploRMI1";

ORemoto.Suma(x,y);

Arquitectura RMI

Servidor:
- Debe extender RemoteObject
- Debe implementar una interfaz diseñada previamente
- Debe tener como mínimo un constructor (nulo) que lance una excepción RemoteException
- El método main debe lanzar un gestor de seguridad, así mismo éste crea los objetos remotos
Cliente:
- De objetos remotos se comunican con interfaces remotas (diseñadas antes de), estos son pasados por referencia
- Los que llamen a métodos remotos deben manejar excepciones

El compilador de RMI (rmic) genera el stub y el skeleton.

Fases de diseño de RMI

Escribir el fichero de la interfaz remota (public y extender de Remote)
Declarar todos los métodos que el servidor remoto ofrece, pero NO los implementa. Se indica nombre, parámentros y topo de retorno.
Todos los métodos de la interfaz remota lanzan obligatoriamente la excepción RemoteException
El propósito de la interface es ocultar la implementación de los aspectos relativos a los métodos remotos, de esta forma, cuando el cliente logra una referencia a un objeto remoto, en realidad obtiene una referencia a una interfaz
Los clientes envían sus mensajes a los métodos de la interfaz

/**
* Ejemplo de implementacion del interfaz remoto para un RMI
*/
import java.rmi.*;
import java.rmi.server.*;
import java.rmi.registry.*;
import java.net.*;
// el servidor debe siempre extender esta clase
// el servidor debe simpre implementar la interfaz
// remota definida con caracter previo
public class EjemploRMI1 extends UnicastRemoteObject implements IEjemploRMI1 {
    public int Suma(int x, int y) throws RemoteException{
        return x + y;
    }

    public int Resta(int x, int y) throws RemoteException {
        return x - y;
    }

    public int Producto(int x, int y) throws RemoteException {
        return x * y;
    }

    public float Cociente(int x, int y) throws RemoteException {
        if (y == 0) return 1 f;
        else return x / y;
    }
    //es necesario que haya un constructor (nulo) como minimo, ya que debe lanzar RemoteException
    public EjemploRMI1() throws RemoteException {
        //super(); invoca automaticamente al constructor de la superclase
    }

    //el metodo main siguiente realiza el registro del servicio
    public static void main(String[] args) throws RemoteException {
        // crea e instala un gestor de seguridad que soporte RMI.
        // el usado es distribuido con JDK. Otros son posibles.
        // En esta ocasion trabajamos sin el.
        // System.setSecurityManager(
        // new RMISecurityManager());
        //Se crea el objeto remoto. Podriamos crear mas si interesa.
        IEjemploRMI1 ORemoto = new EjemploRMI1();

        //Se registra el servicio
        Naming.bind("Servidor", ORemoto);
        System.out.println("Servidor Remoto Preparado");
    }
}

Stub y Skeleton

Es necesario que en la máquina remota donde se aloje el servidor se sitúen también los ficheros stub y skeleton. Con todo ello disponible, se lanza el servidor llamando a JVM del host remoto, previo registro en un DNS.

Registro

Método Naming.bind("Servidor", ORemoto); para registrar el objeto remoto creado requiere que el servidor de nombres esté activo. Dicho servidor se activa con start rmiregistry en Win32, o rmiregistry & en Unix.

Se puede indicar como parámetro el puerto que escucha, si no se indica, por defecto es el puerto 1099. El parámetro puede ser el nombre de un host como por ejemplo:

Naming.bind("//sargo.uca.es:2005/Servidor", ORemoto);

Cliente

El objeto cliente procede siempre creando un objeto de interfaz remota.

Posteriormente efectúa una llamada al método Naming.lookup cuyo parámetro es el nombre y puerto del host remoto junto con el nombre del servidor.

Naming.lookup devuelve una referencia que se convierte a una referencia a la interfaz remota.

A partir de aquí, a través de esa referencia el programador puede invocar todos los métodos de esa interfaz remota como si fueran referencias a objetos en la JVM local.

// Ejemplo de implementacion de un cliente para RMI
import java.rmi.*;
import java.rmi.registry.*;
public class ClienteEjemploRMI1 {
    public static void main(String[] args) throws Exception {
        int a = 10; int b = -10;
        //En esta ocasion trabajamos sin gestor de seguridad //System.setSecurityManager(new RMISecurityManager());
        //Se obtiene una referencia a la interfaz del objeto remoto //SIEMPRE debe convertirse el retorno del metodo Naming.lookup //a un objeto de interfaz remoto
        IEjemploRMI1 RefObRemoto = (IEjemploRMI1) Naming.lookup("//localhost/Servidor");
        System.out.println(RefObRemoto.Suma(a, b));
        System.out.println(RefObRemoto.Resta(a, b));
        System.out.println(RefObRemoto.Producto(a, b));
        System.out.println(RefObRemoto.Cociente(a, b));
    }
}

Evoluciones reseñables

A partir del JDK 1.2 la implementación de RMI no necesita skeletons, el stub estará en ambos lados. A partir del JDK 1.5 se incorpora Generación dinámica de resguardos.

Características avanzadas

Serialización de objetos

Serializar un objeto es convertirlo en una cadena de bits, posteriormente restaurada en el objeto original. Es útil para enviar objetos complejos en RMI.

Los tipos primitivos se serializan automáticamente, las clases contenedoras también. Los objetos complejos deben implementar la interfaz Serializable (es un flag) para poder ser serializados.

Gestión de seguridad(policytool)

Java tiene en cuenta la seguridad, lo ajustamos de la siguiente forma:

System.setSecurityManager(new RMISecurityManager());

Clase RMISecurityManager

Programador ajusta la seguridad mediante la clase Policy

Policy.getPolicy() permite conocer la seguridad actual.
Policy.setPolicy() permite fijar nueva política
Seguridad reside en fichero específico

Java 2 incorpora una herramienta visual: policytool

Ajuste de la política de seguridad, crearlas con policytool.

Para activarlas:

Podemos ejecutar ajustando la política con

java -Djava.security=fichero.policy servidor|cliente

Creando un objeto RMISecurityManager y ajustar SetSecurityManager sobre el objeto creado.

Callback del cliente

Si el servidor RMI debe notificar eventos a clientes, la arquitectura es inapropiada. La alternativa estándar es el sondeo (polling), donde cliente:

Iservidor RefRemota = (IServidor) Naming.lookup (URL);
while (!(Ref.Remota.Evento.Esperado())){}

Características

Clientes interesados se registran en un objeto servidor para que les sea notificado un evento, cuando el evento se produce, el objeto servidor notifica al cliente su ocurrencia.

Para esto hay que duplicar la arquitectura, requiriéndose dos interfaces, habrá dos niveles de stubs:

Cliente (stub+skel) y servidor (stub+skel)

Es necesario proveer en el servidor medios para que los clientes registren sus peticiones de callback.

Descarga dinámica de clases

Permite cambios libres en el servidor, elimina la necesidad de distribuir (resguardos) si los hay y nuevas clases.

Dinámicamente, el cliente descarga todas las clases que necesita para desarrollar una RMI válida, mediante HTTP o FTP.

Novedades a partir de JDK 1.5

Soporta generación dinámica de resguardos, prscinde del generador rmic s

Sistemas de tiempo real. Especificación JRTS

Principios generales de los sistemas de tiempo real

Es un sistema cuyo funcionamiento correcto depende de los resultados lógicos producidos, y también del instante de tiempo en que se producen esos resultados.

El plazo del tiempo dentro del cuál los resultados deben producirse para ser considerados válidos se denominan ligadura temporal. El incumplimiento de esta conlleva aparejado un fallo del sistema.

Objetivo: dar respuesta a eventos procedentes del mundo real antes de un límite temporal establecido (deadline)

Predictibilidad:

Se cumplen los deadlines con independencia de
- Carga de trabajo
- Número de procesadores
- Hilos y prioridades
- Algoritmos de planificación
Determinismo
- Funcionalidad
- Rendimiento
- Tiempo de respuesta

Ejemplos: sistemas de radares, armas de fuego, detección de misiles, etc.

Elementos

En general, incluye sensores (antena radar), sistema de control (hardware, software o combinación de ambos) que lee información procedente de los sensores y efectúa un cálculo con ellos (dentro de la ligadura temporal).

El ciclo habitual del funcionamiento de un STR sigue de forma cíclica las etapas:

lectura de sensores → computación → control de actuadores → actualización del sistema controlado

Propiedades

Reactividad: el sistema interacciona con su entorno, y responde correctamente dentro de su ligadura temporal a los estímulos que los sensores le proporcionan.

Predictibilidad: la ejecución del sistema es determinista, lo cuál implica responder en el plazo adecuado, conocer los componentes software y hardware que se utilizan, y definir marcos temporales acotados cuando no se dispone de un conocimiento temporal exacto.

Fiabilidad: grado de confianza en el sistema, depende de:

Disponibilidad, capacidad de proporcionar servicios cuando se solicitan
Tolerancia a fallos, capacidad de operar en situaciones excepcionales sin causar fallos
Fiabilidad, capacidad de responder siempre igual a la misma situación
Seguridad, capacidad de protegarse frente a ataques o fallos accidentales o deliberados

Tipos

Tipo	Características	Ejemplos
Estrictos(hard)	Respuesta dentro de la ligadura temporal	Control del vuelo de un avión, sistema ABS de frenado
No estrictos, flexibles (soft)	Cumplir la ligadura temporal es el objetivo, pero el sistema puede funcionar bien aunque haya respuestas que no se den en plazo	Sistema de adquisición de datos meteorológicos
Firmes	Se permiten algunos incumplimientos de la ligadura temporal, pero si sonexcesivos el sistema falla de forma total	Sistema de control de reserva de vuelos, sistema de video bajo demanda

Modelo de tareas de RT

Un sistema de TR se estructura en tareas que acceden a los recursos del sistema.

Tarea, conjunto de acciones que describe el comportamiento del sistema o parte ejecutando código secuencial (proceso o hebra).
- Las tareas satisfacen necesidades funcionales concretas
- Tienen definida una ligadura temporal mediante atributos temporales
Recurso, elementos disponibles para la ejecución de tareas.
- Activos: procesador, core, red
- Pasivos: datos, memoria, dispositivos E/S

Atributos temporales de tareas RT

Tiempo de ejecución (C): tiempo necesario para ejecutar la tarea íntegramente.

Tiempo de respuesta (R): tiempo que la tarea ha necesitado para ejecutarse íntegramente.

Ligadura temporal (deadline) (D): máximo tiempo de respuesta posible.

Periodo (T): intervalo temporal entre activaciones sucesivas de tareas periódica.

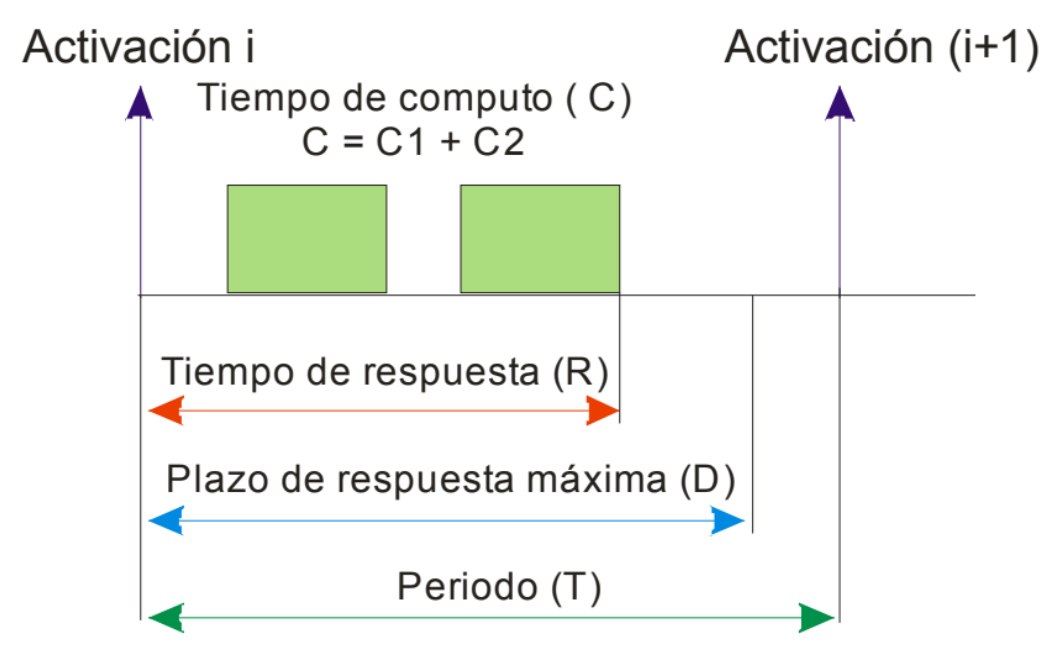
atributos-temporales

Planificación de tareas RT

La planificiación de tareas se encarga de asignar las tareas a los recursos activos de un sistema RT (en especial el procesador o los cores de ejecución), garantizando la ejecución de todas las tareas de acuerdo a las restricciones establecidas. En sistemas RT, estas restricciones aparecen principalmente en forma de ligaduras temporales.

Diseño de la planificación de tareas RT

Para esto debemos:

Determinar los procesadores o cores disponibles a los que podemos asociar tareas
Determinar las relaciones de dependencia entre tareas:
- Relaciones de precedencia entre tareas
- Determinar los recursos comunes a que distintas tareas acceden
Determinar el orden de ejecución de las tareas para garantizar el cumplimiento de las restricciones

Esquema de la planificación de tareas RT

Determinar la planificabilidad de un conjunto de tareas requiere de un esquema (método) de planificación que incluya los siguientes elementos:

Un algorimto de planificación, que define una política de planificación para determinar el orden de acceso de las tareas a los procesadores
Un método de análisis (test de planificabilidad) para predecir el comportamiento temporal del sistema, y determina si la planificabilidad es posible bajo las condiciones o restricciones presentes
Una comprobación factible de que las ligaduras temporales se cumplen en todos los casos posibles

En general, se estudia el peor caso posible o WCET (worst case execution tiempo)

Determinación del WCET

Construir un test de planificabilidad para un conjunto de tareas exige conocer el WCET (C) para cada una de ellas. Es posible determinar este parámetro de dos formas diferentes:

Medimos el tiempo de ejecución en el peor de los casos sobre la plataforma hardware en varias ocasiones y se construye una estadística
Se efectúa un análisis del código ejecutable
- Descomponiendo el código en un grafo de bloques secuenciales
- Calculando el tiempo de ejecución de cada bloque
- Buscando el camino más largo en el grafo

Esquemas de planificación (sistema monoprocesador)

Planificación estática off line sin prioridades, planificación cíclica (ejecutivo cíclico)

Planificación basada en prioridades

Prioridades estáticas
- Prioridad al más frecuente (RMS, rate monotonic scheduling)
- Prioridad al más urgente (DMS, deadline monotonic scheduling)
Prioridades dinámicas
- Proximidad del plazo de respuesta (EDF, earliest deadline first)
- Prioridad al de menor olgura (LLF, least laxity first)

Ejemplo de planificación cíclica

Construye una planificación explícita y fuera de línea de las tareas que especifica el entrelazado de las mismas forma que su ejecución cíclica garantiza que se cumplen las ligaduras temporales.

La estructura de cntrol se denomida ejecutivo cíclico. El entrelazado de tareas es fijo, y conocido antes de poner en marcha el sistema.

La duración del ciclo principal es igual al hiperperiodo $T_M = mcm(T_1, T_2, ..., T_m)$, se suponen tiempo entero, y el comportamiento temporal del sistema se repite cada ciclo principal.

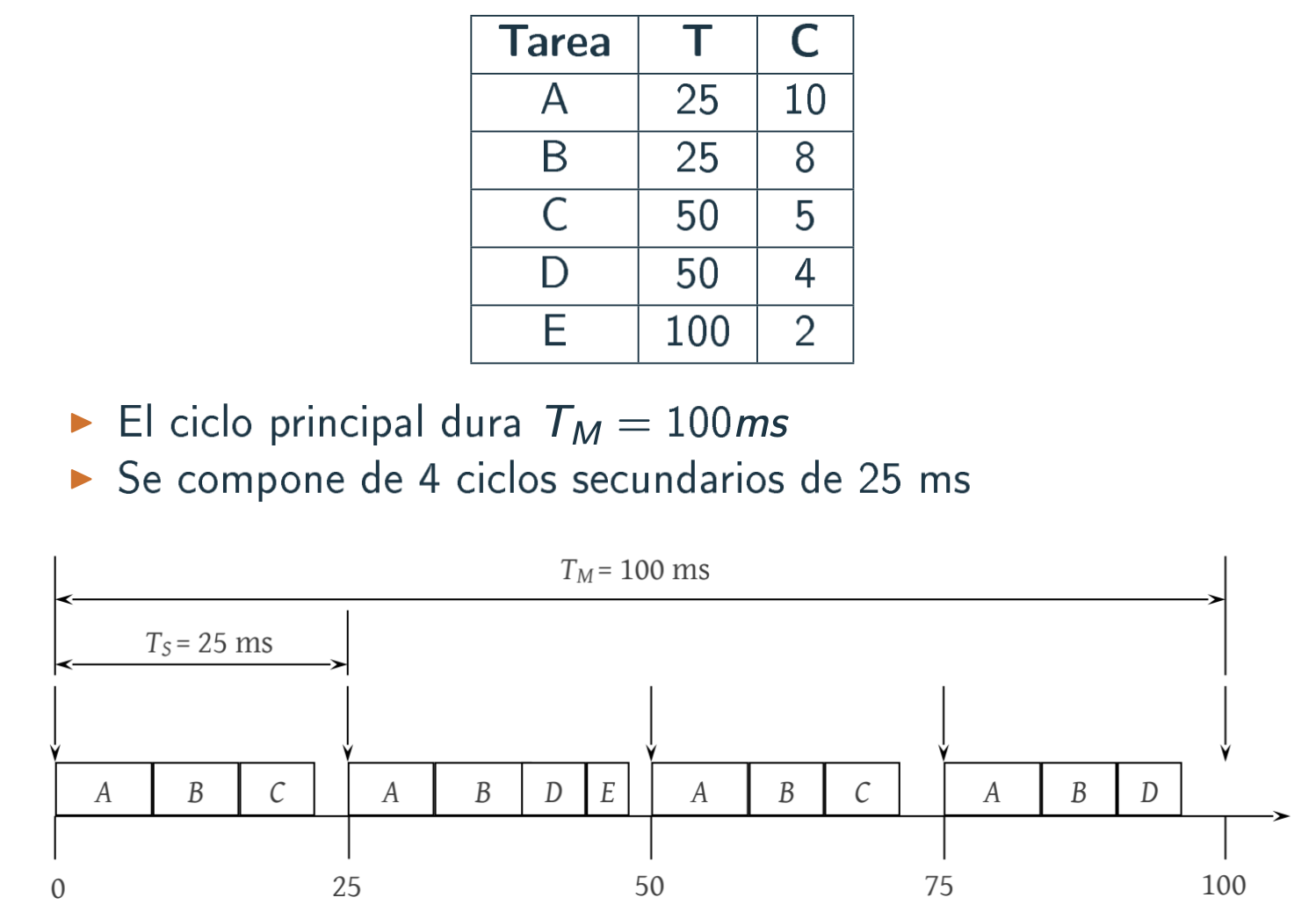
planificación-cíclica

Propiedades de la planificación cíclica

NO hay concurrencia en la ejecución, cada ciclo secundario en una secuencia de llamadas a método. No se necesita un núcleo de ejecución multitarea.

Las tareas pueden compartir datos, sin tener que llevar control de exclusión mutua. No necesitamos analizar el comportamiento temporal.

Inconvenientes de la planificación cíclica

Dificultad para incorporar tareas con periodos largos, las tareas esporádicas dificultan el tratamiento.

El plan del ciclo es difícil de construir, poco flexible y de difícil mantenimiento.

Planificación con prioridades

La prioridad es un atributo de las tareas que mide su importancia relativa respecto a las demás, se codifica con números enteros cecientes según la importancia de la tarea (o al revés). La prioridad de una tarea determina sus necesidades temporales.

Idealmente, las tareas se despachan para ejecución según su prioridad

Prioridades RMS

Método de planificación estático online con asignación de prioridades a las tareas más frecuentes.

Cada tarea recibe una prioridad única basada en su periodo; cuanto menor sea el periodo (mayor frecuencia), mayor prioridad. $\forall i,j: T_i < T_j → P_i < P_j$.

Aquí asignamos prioridades decrecientes para procesos más frecuentes.

Prioridades EDF

Da mayor prioridad a la tarea más próxima a su ligadura temporal (deadline). En caso de igualdad, se hace una elección no determinista.

Es un algoritmo de planificación dinámico, donde las prioridades de las tareas cambian en el tiempo. No necesita que las tareas sean periódicas.

Límites de Java estándar en RT

Gestión de memoria
- gc, recolector de basura, es impredecible. Se activa cuando quiere
- Fragmenta la memoria (memoria no planificable)
Planificación de Threads
- Impredecible
- No permite especificar cuándo un hilo ha de ejecutarse
- Inversiones de prioridad
Sincronización
- Duración de secciones críticas impredecible
- Un hilo no sabe cuántas otras tareas compiten por un recurso ni su prioridad
Gestión asíncrona de eventos (no definida)
Acceso a memoria física
- Una tarea no sabe cuánta hay ni cuánta necesita

La especificación Java-RT (RTJS)

Cambia la JVM para que soporte RT, no modifica el lenguaje Java; lo engloba.

Incorpora:

Tipos nuevos de hilos
Tipos nuevos de memoria
Gestión asíncrona de eventos
Predictibilidad (fente a rendimiento)

Conservando:

Compatibilidad hacia atrás
El lenguaje y el bytecode

Gestión de memoria: API

RTJS provee áreas de memoria no afectadas por gc, al existir fuera del heap. El gc puede ser expulsado por un hilo RT.

Se utiliza la clase abstracta MemoryArea y sus subclases:

HeapMemory, InmortalMemory, ScopedMemory; VTMemory, LTMemory

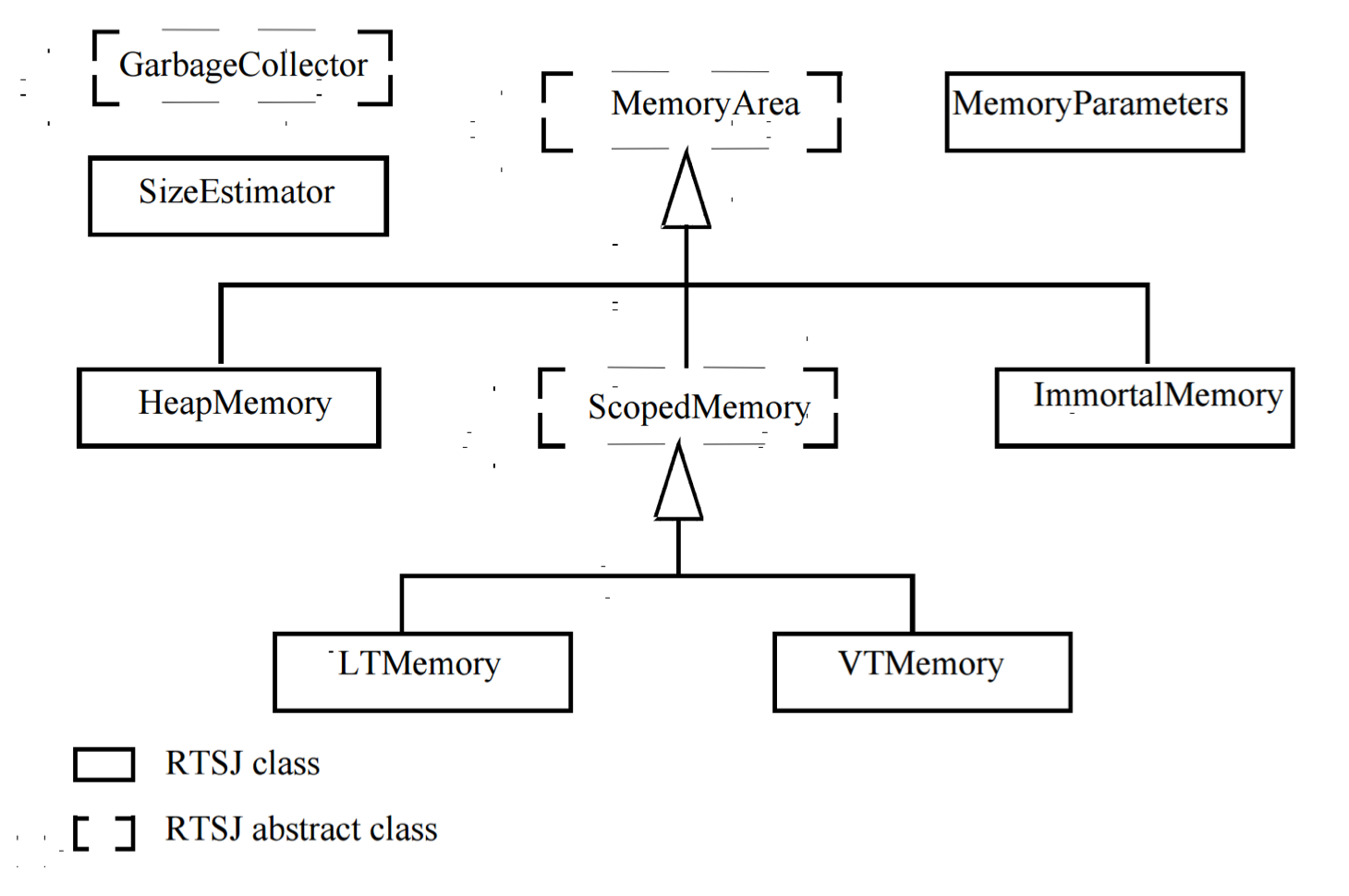
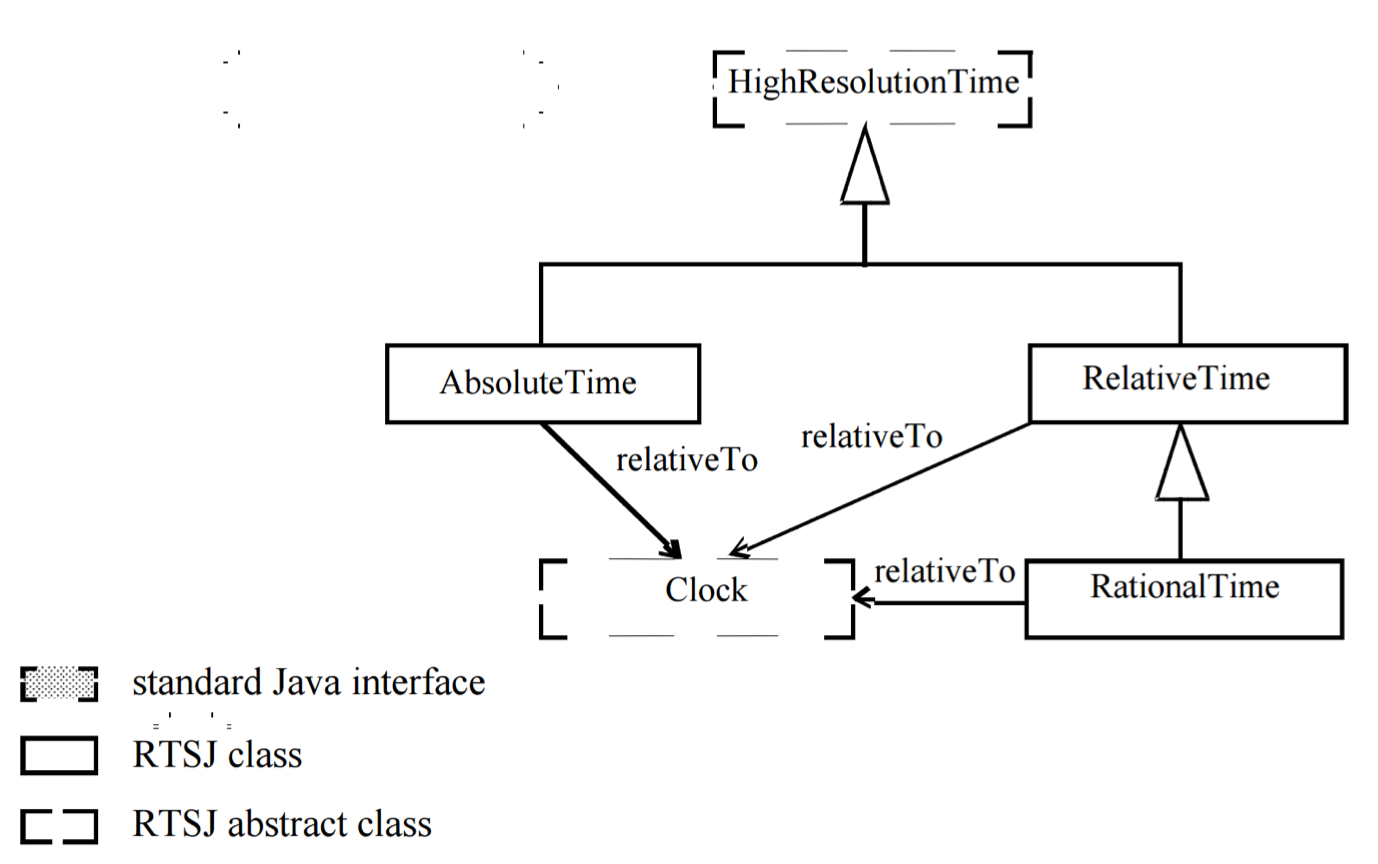
memoria:clases

Planificación en Java, limitaciones

Java no garantiza que los hilos de alta prioridad se ejecuten antes, debido a el mapping hilos_java-hilos_sistema y el uso de planificación no expulsiva.

El esquema de diez prioridades java cambia durante el mapping a prioridades de sistema, con superposiciones dependientes del sistema.

El concepto de planificación por prioridad es tan débil que lo hace completamente inadecuado para su uso en entornos RT. Por tanto, los hilos de mayor prioridad, eventualmente se ejecutarán antes, pero NO hay garantías de que ello ocurra así.

Planificación en Java-RT: Gold standard

Planificación por prioridades fijas, preemtive (expulsivo) y con 28 niveles de prioridad.

Fijas, porque los objetos planificables no cambian su prioridad (salvo si hay inversión de prioridad → herencia de prioridad)
Expulsiva, porque el sistema puede sacar, por diferentes motivos, al objeto en ejecución

Objetos planificables, `Schedulable`

RTJS generaliza el concepto de entidades ejecutables desde el conocido thread a los objetos planificables schedulable objects.

Un objeto planificable implementa la interfaz Schedulable y puede ser:

Hilos RT (clase RealTimeThread y NoHeapRealTimeThread)
Gestores de eventos asíncronos (clase AsyncEventHandles)

Cada objeto planificable debe especificar sus requerimientos temporales, indicando requerimientos de:

Lanzamiento (release)
Memoria (memory)
Planificación (schedulng)

Parámetros de lanzamiento (`release`)

Tipos de lanzamiento:

Periódico, activación por intervalos regulares
Aperiódico, activación aleatoria
Esporádico, activación irregular con un tiempo mínimo entre dos activaciones

Todos los tipos de lanzamiento tienen un coste y un deadline relativo:

El coste es el tiempo de CPU requerido para cada activación
El deadline es el límite de tiempo dentro del cual la actiación actual debe haber finalizado

Lanzamiento de un hilo RT:

RealtimeThread htr = new RealTimeThread();
RelativeTime miliseg = new RelativeTime(1,0);
ReleaseParameters relpar = new Periodic Parameters(miliseg);
htr.setReleaseParameters(relpar);

Parámetros de planificación (`scheduling`)

Son utilizados por el planificador para escoger qué objeto planificable ha de ejecutarse. Se utiliza la clase abstracta SchedulingParameters como la raíz de una jerarquía que permite múltiples parámetros de planificación.

RTJS utiliza como criterio de planificación único la prioridad, de acuerdo al gold standard

Clases: PriorityParameters, ImportanceParameters

Ajuste de prioridad de un hilo RT:

RealtimeThread htr = new RealTimeThread();
int maxPri = PriorityScheduler.instance().getMaxPriority();
PriorityParameters pri = new PriorityParameters(maxPri);
htr.setSchedulingParameters(pri);

Planificadores (`schedulers`)

Son los algoritmos responsables de planificar para ejecución los objetos planificables. RTJS soporta planificación expulsiva por prioridades de 28 niveles mediante el PriorityScheduler

Scheduler es una clase abstracta (una instancia única por JVM y PriorityScheduler es una subclase).

Este esquema permite el diseño de planificadores propios mejorados.

clases-planificacion

Cumplimiento de deadlines

Un sistema de tiempo real bien diseñado debe predecir si los objetos de aplicación cumplirán sus deadlines y evitar la pérdida de deadlines y sobrecargas de ejecución.

Algunos sistemas pueden ser verificados offline, otros requieren un análisis online. RTJS provee herramientas para el análisis online.

Threads Real-Time: Generalidades

Son objetos schedulable y heredan de la clase Thread, mucho más que una simple extensión de la clase, existe además una versión no-heap independiente del recolector de basura y que no usa memoria del heap.

threads-rt

Gestión de eventos asíncronos: Generalidades

Threads estándares o RT modelan bien tareas concurrentes con un ciclo de vida bien definido. Se requiere modelar eventos que ocurren asíncronamente durante la actividad de un hilo, procedentes del entorno o generados por la lógica del programa.

Podríamos tener hilos en espera (p.e: en un pool) para tratarlos, pero sería ineficiente.

Desde un enfoque RT, estos eventos requieren gestores que respondan bajo un deadline, RTJS generaliza los gestores de eventos a objetos schedulable.

manejadores-eventos

Hilos RT y manejadores de eventos

En la práctica, la JVM-RT liga dinámicamene un gestor de eventos con un hilo-rt. Es posible, ligar un gestor de eventos a un hilo-rt de forma permanente.

Cada instancia de AsyncEvent puede tener más de un gestor de eventos. Cuando el evento se produce, su gestor de eventos es activado para ejecución según sus parámetros de planificación.

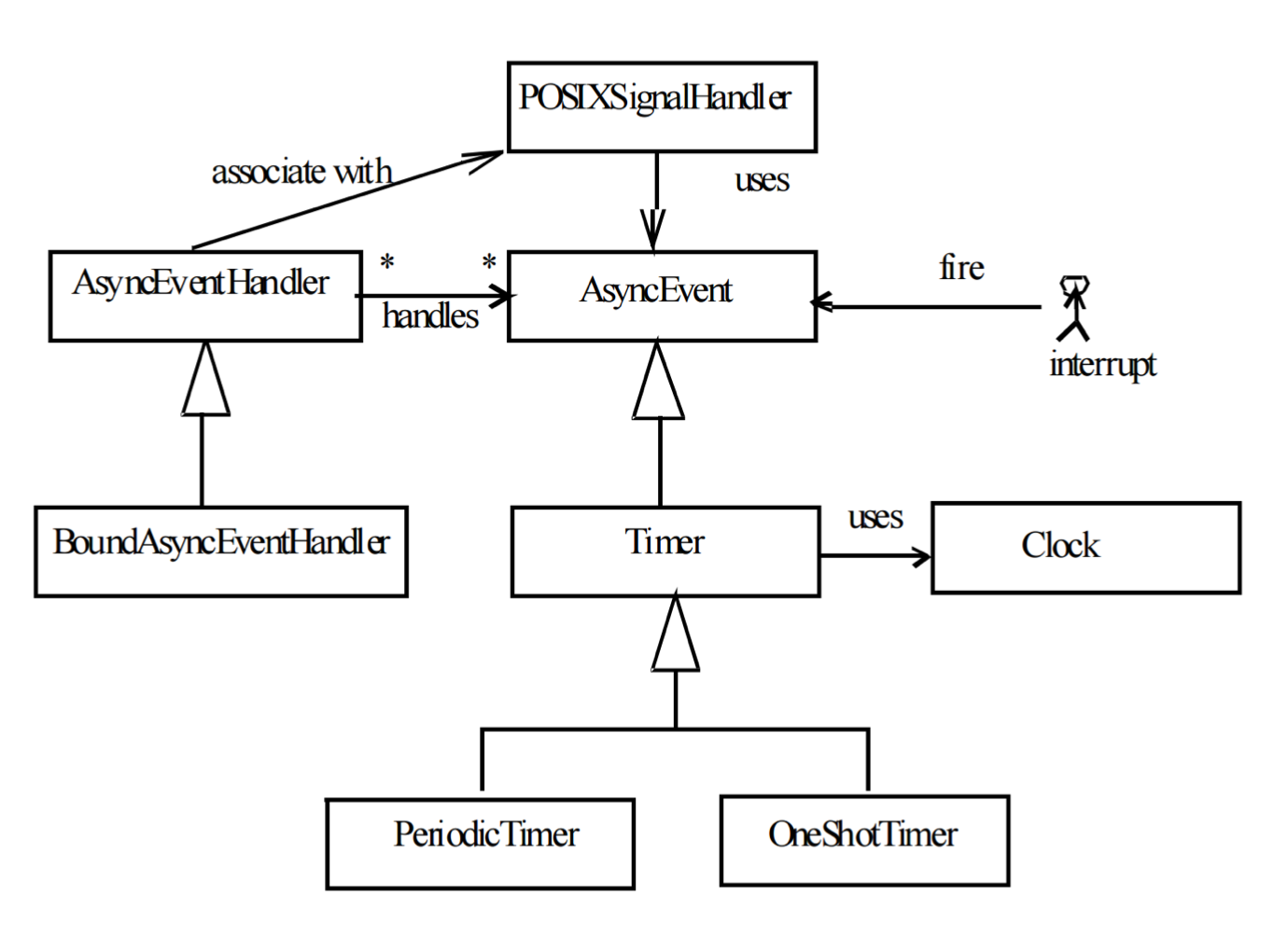
eventos-asincronos

Control de la sincronización

Los objetos planificables (incluidos hilos-rt) deben poderse comunicar y sincronizar. Sabemos que Java proporciona control de acceso tipo monitos a objetos para control de la E.M. Sin embargo, todas las técnicas de sincronización basadas en la E.M. sufren inversión de prioridades.

Java-RT lo soluciona mediante la técnica de herencia de prioridad

herencia-prioridades

Seminarios

Programación concurrente con C++17

Biblioteca `Thread`

C++ introduce a partir de la iteración de 2011 una nueva biblioteca para gestión de hebras concurrentes: <thread>. Permite la creación y ejecución de hebras como objetos de clase thread.

También da soporte al programador para sincronizar hebras mediante cerrojos de la clase mutex, y más complejos; disponible el uso de variables atómicas, y se ofrecen monitores con semántica de señalización SC y variables de condición.

Creación y ejecución de hebras

Creamos una instancia de la clase std::thread, utilizando como parámetro la función (en realidad, lo que se transfiere es un puntero a dicha función) que contiene el código que deseamos que la hebra ejecute.

El uso del contructor de clase tiene un doble efecto; no sólo crea el nuevo objeto, sino que también lo arranca de forma automática.

std::thread nombre(tarea);

nombre es la referencia al nuevo objeto de clase thread que estamos creando, y tarea es la función que contiene el código que la nueva hebra debe ejecutar.

Técnicas de creación

Además de la técnica anterior, podemos utilizar funciones lambda (función anónima), para el caso de que el código que la hebra a ejecutar sea muy pequeño, y no necesitemos escribir una función para contenerlo.

#include <vector>
#include <iostream>
#include <thread>

void hello() {
    std::cout << "Hello from thread" << std::this_thread::get_id() << std::endl;
}

int main() {
    std::vector<std::thread> threads;

    for(int i = 0; i < 5; ++i) {
        threads.push_back(std::thread(hello));
    }

    for(auto& thread : threads){
        thread.join();
    }
    return 0;

}

// Corrutina múltiple con array de hebras
#include <thread>
#include <iostream>
#include <vector>

auto hello() -> void {
    std::cout << "Hello from thread " << std::this_thread::get_id() << std::endl;
}

auto main() -> int {
    std::vector<std::thread> threads(100);
    for (auto & thread : threads) {
        thread = std::thread(hello);
    }

    for (auto& thread: threads) {
        thread.join();
    }

    std::cout << "Hello from main thread " << std::this_thread::get_id() << std::endl;
    return 0;
}

Gestionando las hebras

En general, el programador puede necesitar determinadas operaciones de gestión de sus hebras concurrentes como son:

Hacer que una hebra espera a que termina otra (método join)
Hacer que una hebra espere un tiempo determinado "durmiendo"
Asignar prioridades a las hebras para alterar el orden en que se ejecuten
Interrumpir la ejecución de una hebra

"Durmiendo" hebras, método `sleep_for`

Tiene como parámetro el tiempo de sueño habitualmente expresado en milisegundos (hace falta #include <chrono>). Admite otras unidades de media temporal, no es útil para planificar de manera adecuada.

std::chrono::milliseconds duracion(2000);
std::this_thread::sleep_for(duracion);

Replanificación voluntaria, método `yield`

Una hebra puede "insinuar" al planificador que puede ser replanificada, permitiendo que otras se ejecuten. El comportamiento exacto del método yield depende de la implementación y, en particular, del funcionamiento del planificador del SO.

No es una técnica de planificación adecuada, y es poco utilizada en la práctica

Técnicas de control de EM y sincronización en C++

C++ ofrece una amplia variedad de técnicas de control de la EM (y de sincronización) que incluyen:

Cerrojos y cerrojos reentrantes
Objetos atómicos
Monitores
Variables de condición (dentro de monitor)

Control de EM con cerrojos mutex:

C++ proporciona cerrojos mediante la clase mutex
La sección crítica se encierra entre los métodos lock() y unlock()
No provee cerrojos reentrantes, lo cuál los hace inútil en programas recursivos

Ejemplos:

#include <mutex>

struct Cuenta {
    int val =0;
    std::mutex cerrojo;
    void inc () {
        cerrojo.lock();
        val++;
        cerrojo.unlock();
    }

    // Otra forma de escribirlo
    void inc () {
        std::lock_guard<std::mutex> cerrojo(mutex);
        val++;
    }
}

Los objetos mutex carecen de reentrancia

Cerrojos reentrantes: `recursive_mutex`

La sección crítica se encierra entre los métodos lock() y unlock(). Ahora la posesión del bloqueo es por hebra, lo cuál permitra llamadas recursivas o llamadas entre funciones diferentes que tiene todo (o parte) de su código bajo exclusión mutua controlada por el mismo cerrojo recursivo.

El cerrojo puede ser adquirido varias veces por la misma hebra

std::recursive_mutex mutex;

void inc () {
    std::lock_guard<std::recursive_mutex> cerrojo(mutex);
    val++;
}

Limitando el acceso a una sola vez: `call_once`

En ocasiones, interesa limitar a una única vez el número de veces que una función puede ser llamada, con independencia del número de hebras que la utilicen. Para ella, se puede utilizar la función call_once, que tiene el siguiente prototipo:

std::call_once(flag, funcion);

Aquí flag es un objeto de clases std::once_flag, que nos proporciona la semántica de "llamada una sola vez" sobre el código que se encuentra en el parámetro funcion.

// Establecemos la bandera de tipo once_flag
std::once_flag bandera;

void hacer_algo () {
    //el mensaje siguiente solo se mostrar una vez.
    std::call_once(bandera, [](){ std::cout << "Lamado una vez" << std::endl; });
    //Se mostrara tantas veces como hilos tengamos
    std::cout<<"Llamado cada vez"<<std::endl;
}

Tipos atómicos

La biblioteca <atomic> proporciona componentes para efectuar operaciones seguras sobre secciones críticas de grano fino (muy pequeñas), cada operación atómica es indivisible frente a otras operaciones atómicas sobre el mismo dato.

Los datos procesados de esta forma están libre de condiciones de carrera, es posible aplicar atomicidad sobre información compartida tanto sobre datos de tipo primitivo, como sobre datos definidos por el programador.

#include <atomic>

// se define el objeto atomico
std::atomic<int> x;

Monitores

En C++, un monitor es un objeto donde todos los métodos se ejecutan en EM bajo el control de un mismo cerrojo.

Si es necesario, es posible disponer de varias variables de condición, para hacer esperar a hebras por condiciones concretas. En tal caso, el cerrojo a utilizar deberá ser de clase unique_lock, la cuál permite instanciar variables de condición.

En caso de utilizar variables de condición, la semántica de señalización del monitor es SC, lo que obliga al uso de condiciones de guarda.

Memoria Transaccional Software con Clojure/Java

STM

Técnica de control de la concurrencia alternativa al modelo de bloqueos, similar al sistema de transacciones de una BD. Las operaciones sobre datos compartidos se ejecutan dentro de una transacción, lo cuál permite:

Disponer de operaciones libres de bloqueos (e interbloqueos)
Aumentar el paralelismo en el acceso a los datos compartidos
Evitar las condiciones de concurso continuas sobre un mismo cerrojo

La STM simplifica la p.concurrente sustituyendo el acceso a datos compartidos bajo control de cerrojo, por el acceso a los mismos dentro de una transacción.

Concepto de transacción

Una transacción es una secuencia de operaciones desarrolladas por una tarea concurrente (proceso o hebra) sobre un conjunto de datos compartidos que puede terminar de dos maneras:

Validando (commit) las transacciones, todas las actualizaciones efectuadas por la tarea sobre los datos compartidos tienen efecto atómico
Abortando la transacción, los cambios no tienen efecto y los datos no cambian. Típicamente la transacción se intenta de nuevo (roll-back)

Las transacciones habitualmente cumplen las conocidas propiedades ACID:

Atomicidad
Consistencia
Aislamiento
Durabilidad

Desde un punto de vista técnico

El marco que da soporte a la STM no es técnicamente sencillo, ya que

Debe garantizar la ejecución atómica de las transacciones
Asegura que se cumple ACID y todo ello sin usar cerrojos

Se propone enfoques basados en hardware, en software e híbridos para soportar técnicamente el econcepto de memoria transaccional software, para Java, hay decenas de implementaciones posibles.

Todo lenguaje o API que soporte STM necesita un manejador de transacciones, que es el algoritmo que se encarga de procesor las transacciones que el programador escribe garantizando las propiedades ACID.

Algoritmo de procesamiento de transacción

Algoritmo de procesamiento de una Transaccion

Inicio
Hacer copia privada de los datos compartidos
Hacer actualizaciones en la copia privada
Ahora:
- Si datos compartidos no modificados → actualizar datos compartidos con copia privada y goto(Fin)
- Si hay conflictos, descartar copia privada y goto(Inicio)
Fin

STM con el lenguaje Clojure

Con clojure, los valores, estados, son inmutables y las identidades únicamente pueden cambiar dentro de una transacción

ref permite crear identidades mutables

def no es únicamente válido para funciones, sino que es aplicable a cualquier tipo. Nosotros la utilizarremos junto a ref

Transacciones con Clojure

Una transacción se crea envolviendo el código de interés (que normalmente serán los datos compartidos) en un bloque dosync de forma parecida a la que hacíamos con synchrinized en Java.

OJO, no es lo mismo

Dentro del bloque podemos cambiar el estado de la entidad:

Utilizando ref-set que establece el nuevo estado de la identidad y lo devuelve
Utilizando alter que establece el nuevo estado de la identidad como el resultado de aplicar una función y lo devuelve

(def balance (ref 0))
(println "El saldo es " @balance)
(dosync( ref-set balance 100 )) ; sin dosync no funciona
(println "El saldo es ahora " @balance)

Clojure en Java

Clojure es interpretado por la JVM, por lo que existe cierto grado de compatibilidad entre Java y Clojure. Si utilizamos la API de Clojure, en Java podemos tener disponibles dos nuevas clases:

La clase Ref que sirve para que una identidad se asocia a un estado (valor) en el ambiente de Clojure.
La clase LockingTransaction que proporciona, entre otros, el método runInTransaction, cuyo parámetro es un objeto que implementa la interfaz Callable (es decir, una tarea concurrente), y que la ejecuta dentro de una transacción, gracias al manejador de transacciones de Clojure.

Programación concurrente con Python

Monitores

Es posible disponer de monitores SC en Python, se estructuran en torno a la clase Condition. Un objeto de clase Condition soporta un cerrojo y un único wait-set.

Es un modelo similar al de monitores en Java con el API de concurrencia estándar, es por tanto, obligado el uso de condiciones de guarda.

Este modelo de hebras...

Python utiliza el Global Interpreter Lock (GIL). Los cual imposibilita el paralelismo real, olbiga a las hebras a ejecutarse secuencialmente e imposibilita ligrar speedups mayores a 1.

Concurrencia con procesos

Alternativa a threading y el GIL, usando el módulo multiprocessing. Libre del GIL → concurrencia real, pero a diferencia de las hebras los procesos no comportan memoria, se necesitan medios específicos (IPC) para compartir la memoria.

Instanciar un proceso rápidamente

Utilizando el contructor de la clase Process, recibe dos parámetros:

Una función/método con el código que el proceso debe ejecutar
La lista de parámetros que la función/método necesita

multiprocessing.Process(target=miFuncion, args=(arg1, arg2,..., argn))

multiprocessing crea dos intérpretes de python

PCTR 2020