Udding’s starvation-free algorithm

There are solutions to the critical-section problem using weak semaphores that are free of starvation. We give without proof a solution developed by Jan T. Udding [68]. Algorithm 6.14 is similar to the fast algorithms described in Section 5.4, with two gates that must be passed in order to enter the critical section.

The two semaphores constitute a split binary semaphore satisfying \(0 < gate1 + gate2 < 1\), and the integer variables count the number of processes about to enter or trying to enter each gate.

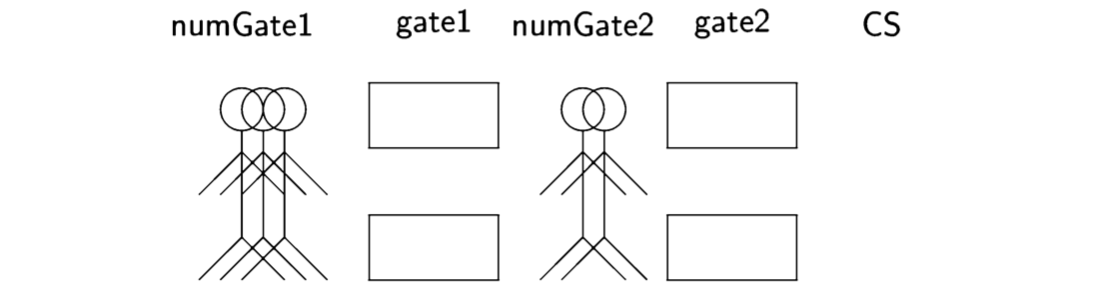
The semaphore gatel is reused to provided mutual exclusion during the initial increment of numGate1. In our model, where each line is an atomic operation, this protection is not needed, but freedom from starvation depends on it so we have included it.

The idea behind the algorithm is that processes successfully pass through a gate (complete the wait operation) as a group, without interleaving wait operations from the other processes. Thus a process p passing through gate2 into the critical section may quickly rejoin the group of processes in front of gate1, but all of the colleagues from its group will enter the critical section before p passes the first gate again. This ensures that the algorithm is free from starvation.

The attempted solution still suffers from the possibility of starvation, as shown by the following outline of a scenario:

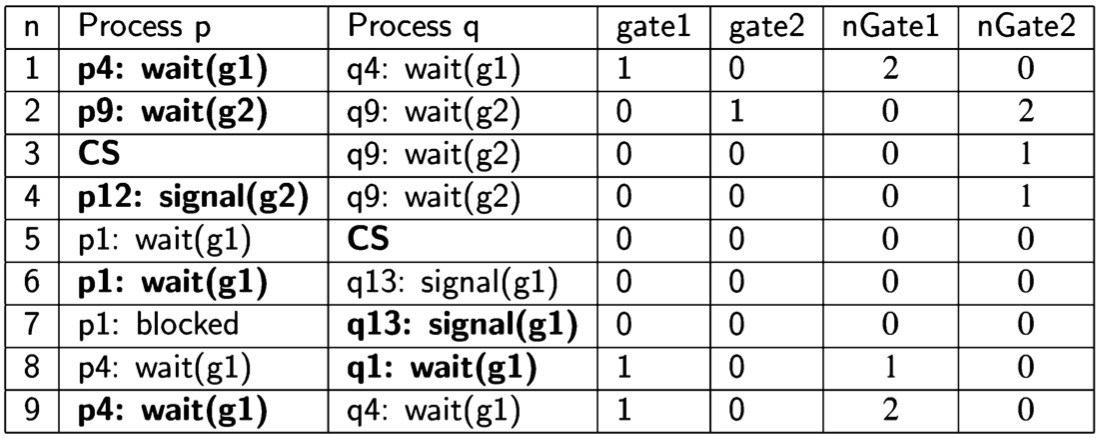
Two processes are denoted p and q with appropriate line numbers; the third process r is omitted because it remains blocked at rl: wait(g1) throughout the scenario. Variable names have been shortened: gate to g and numGate to nGate.

The scenario starts with processes p and q at gates p4 and q4, respectively, while the third process r has yet to pass the initial wait operation at r1. The key line in the scenario is line 7, where q unblocks his old colleague p waiting again at p1 instead of r who has been waiting at r1 for quite a long time.

By adding an additional semaphore, we can ensure that at most one process is at the second gate at any one time. The semaphore onlyOne is initialized to 1, a wait(onlyOne) operation is added before p4 and a signal(onlyOne) operation is added before p9. This ensures that at most one process will be blocked at gate1.