The critical section problem for N processes

Using semaphores, the same algorithm gives a solution for the critical section problem for N processes:

The proofs in Theorem 6.2 remain unchanged for N processes as far as mutual exclusion and freedom from deadlock are concerned. Unfortunately, freedeom from starvation does not hold. For the abbreviated algorithm:

consider the following scenario for three processes, where the statement numbers for processes q and r correspond to those for p in Algorithm 6.4:

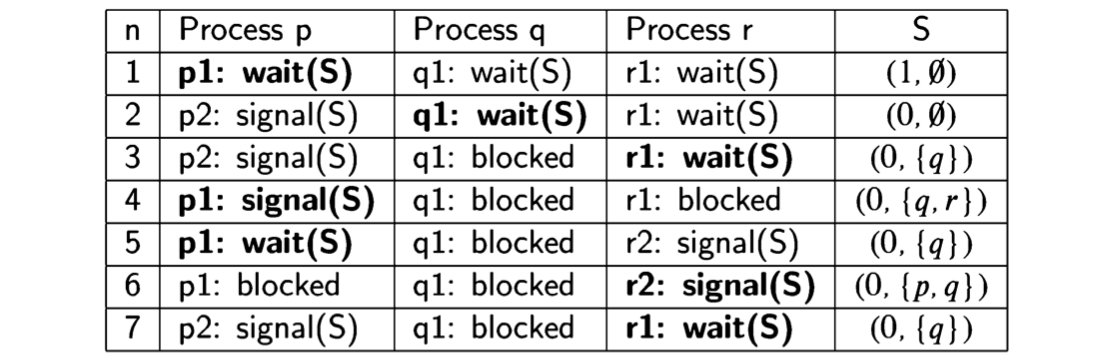
Line 7 is the same as line 3 and the scenario can continue indefinitely in this loop of states. The two processes p and r conspire to starve process q.

When there were only two processes, we used the fact that S.L is the singleton set {p} to claim that process p must be unblocked, but with more than two processes this claim no longer holds. Starvation is caused by the fact that, in our definition of the semaphore type, a signal operation may unblock an arbitrary element of S.L. Freedom from starvation does not occur if the definition of the semaphore type is changed so that S.L is a queue not a set. (See Section 6.8 for a comparison of semaphore definitions.)

In the exercises, you are asked to show that if the initial value of S.V is k, then at most k processes can be in the critical section at any time.