Second attempt

The first attempt was incorrect because both processes set and tested a single global variable. If one process dies, the other is blocked. Let us try to solve the critical section problem by providing each process with its own variable (Algorithm 3.6). The intended interpretation of the variables is that wanti is true from the step where process i wants to enter its critical section until it leaves the critical section. await statements ensure that a process does not enter its critical section while the other process has its flag set. This solution does not suffer from the problem of the

previous one: if a process halts in its non-critical section, the value of its variable want will remain false and the other process will always succeed in immediately entering its critical section.

Let us construct a state diagram for the abbreviated algorithm:

Unfortunately, when we start to incrementally construct the state diagram (Fig- ure 3.4), we quickly find the state (p3: \( wantp \leftarrow false \), q3: \(wantq \leftarrow false\), true, true), showing that the mutual exclusion property is not satisfied. (await !want is used instead of await want=false because of space constraints in the node.)

Paths in the state diagram correspond to scenarios; this portion of the scenario can also be displayed in tabular form:

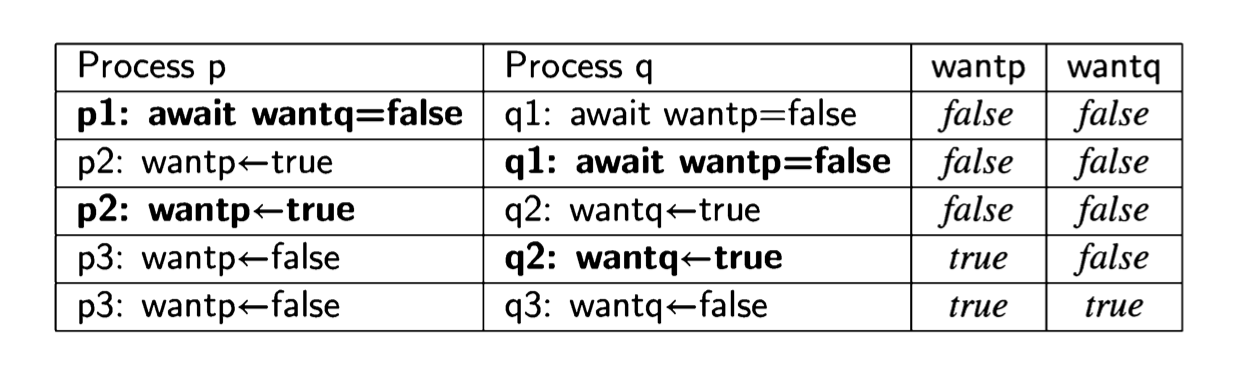
To prove that mutual exclusion holds, we must check that no forbidden state appears in any scenario. So if mutual exclusion does in fact hold, we need to construct

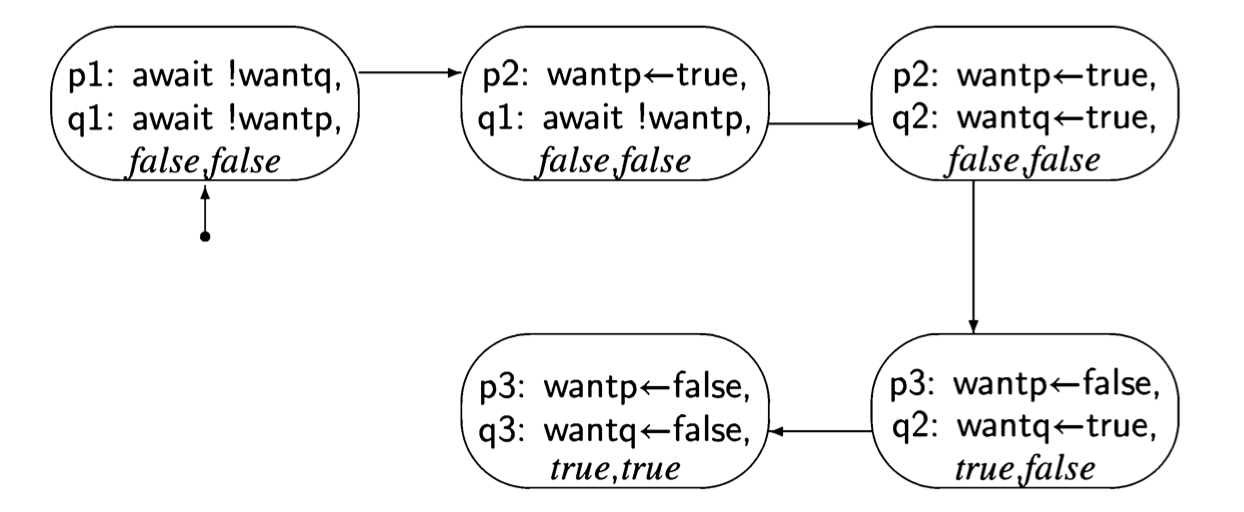
the full state diagram for the algorithm, because every path in the diagram is a sce- nario; then we must examine every state to make sure that it is not a forbidden state. When constructing the diagram incrementally, we check each state as it is created, so that we can stop the construction if a forbidden state is encountered, as it was in this case. It follows that if the incremental construction is completed (that is, there are no more reachable states), then we know that no forbidden states occur.