The definition of the problem
We start with a specification of the structure of the critical section problem and the assumptions under which it must be solved:
-
Each of N processes is executing in a infinite loop a sequence of statements that can be divided into two subsequences: the critical section and the non- critical section.
-
The correctness specifications required of any solution are:
-
Mutual exclusion Statements from the critical sections of two or more pro- cesses must not be interleaved.
-
Freedom from deadlock If some processes are trying to enter their critical sections, then one of them must eventually succeed.
-
Freedom from (individual) starvation If any process tries to enter its crit- ical section, then that process must eventually succeed.
-
-
A synchronization mechanism must be provided to ensure that the correctness requirements are met. The synchronization mechanism consists of additional statements that are placed before and after the critical section. The statements placed before the critical section are called the preprotocol and those after it are called the postprotocol. Thus, the structure of a solution for two processes is as follows:
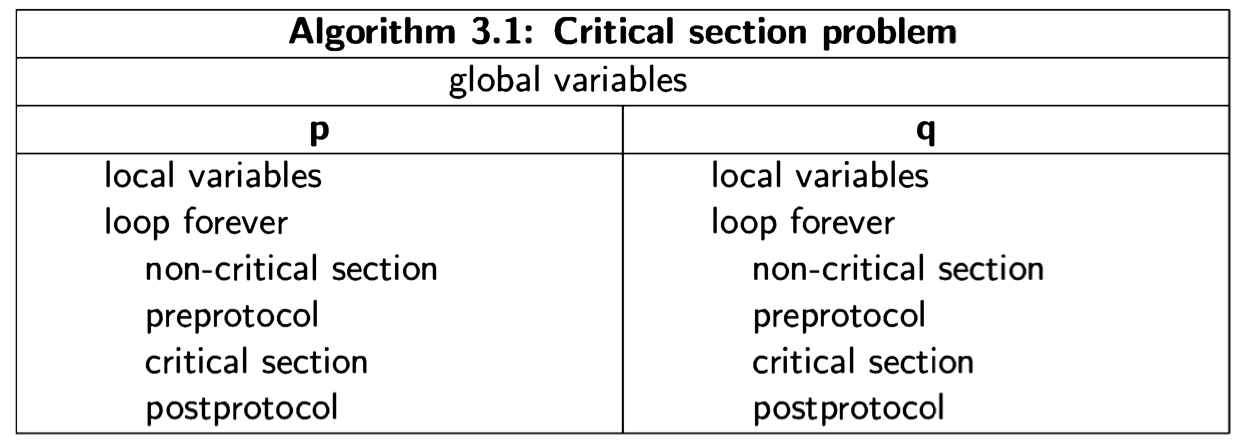
-
The protocols may require local or global variables, but we assume that no variables used in the critical and non-critical sections are used in the proto- cols, and vice versa.
-
The critical section must progress, that is, once a process starts to execute the statements of its critical section, it must eventually finish executing those statements.
-
The non-critical section need not progress, that is, if the control pointer of a process is at or in its non-critical section, the process may terminate or enter an infinite loop and not leave the non-critical section.
The following diagram will help visualize the critical section problem:
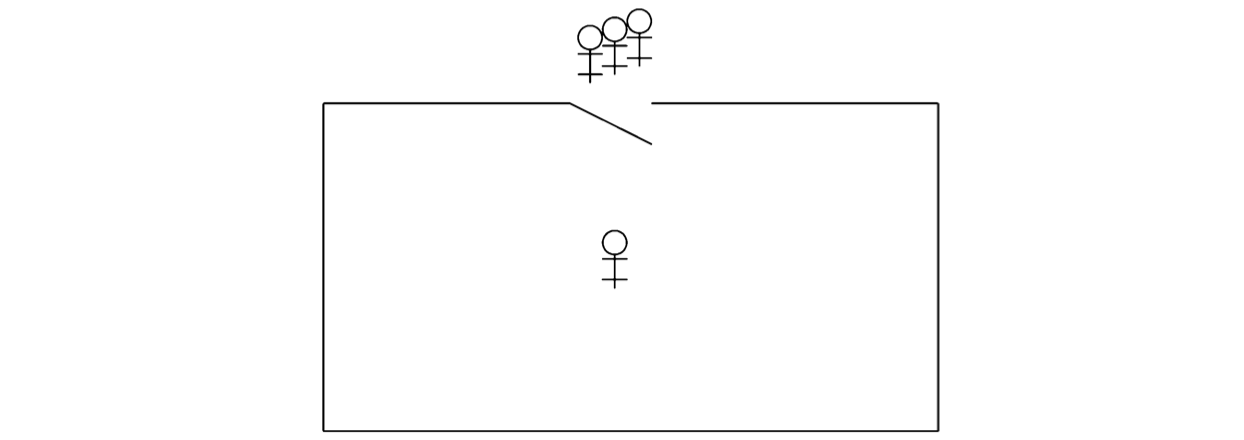
The stick figures represent processes and the box is a critical region in which at most one process at a time may be executing the statements that form its critical section. The solution to the problem is given by the protocols for opening and closing the door to the critical region in such a manner that the correctness properties are satisfied.
The critical section problem is intended to model a system that performs complex computation, but occasionally needs to access data or hardware that is shared by several processes. It is unreasonable to expect that individual processes will never terminate, or that nothing bad will ever occur in the programs of the system. For example, a check-in kiosk at an airport waits for a passenger to swipe his credit card or touch the screen. When that occurs, the program in the kiosk will access a central database of passengers, and it is important that only one of these programs update the database at atime. The critical section is intended to model this operation only, while the non-critical section models all the computation of the program except for the actual update of the database.
It would not make sense to require that the program actually participate in the
update of the database by programs in other kiosks, so we allow it to wait indefinitely
for input, and we take into account that the program could malfunction. In other
words, we do not require that the non-critical section progress. On the other hand,
we do require that the critical section progress so that it eventually terminates. The
reason is that the process executing a critical section typically holds a lock or
permission resource, and the lock or resource must eventually be released so that
other processes can enter their critical sections. The requirement for progress is
reasonable, because critical sections are usually very short and their progress can
be formally verified.
Obviously, deadlock (my computer froze up) must be avoided, because systems
are intended to provide a service. Even if there is local progress within the
protocols as the processes set and check the protocol variables, if no process ever
succeeds in making the transition from the preprotocol to the critical section, the
program is deadlocked.
Freedom from starvation is a strong requirement in that it must be shown that no possible execution sequence of the program, no matter how improbable, can cause starvation of any process. This requirement can be weakened; we will see one example in the algorithm of Section 5.4.
A good solution to the critical section problem will also be efficient, in the sense that the pre- and postprotocols will use as little time and memory as possible. In particular, if only a single process wishes to enter its critical section it will succeed in doing so almost immediately.