Dekker's algorithm

Dekker’s algorithm for solving the critical section problem is a combination of the first and fourth attempts:

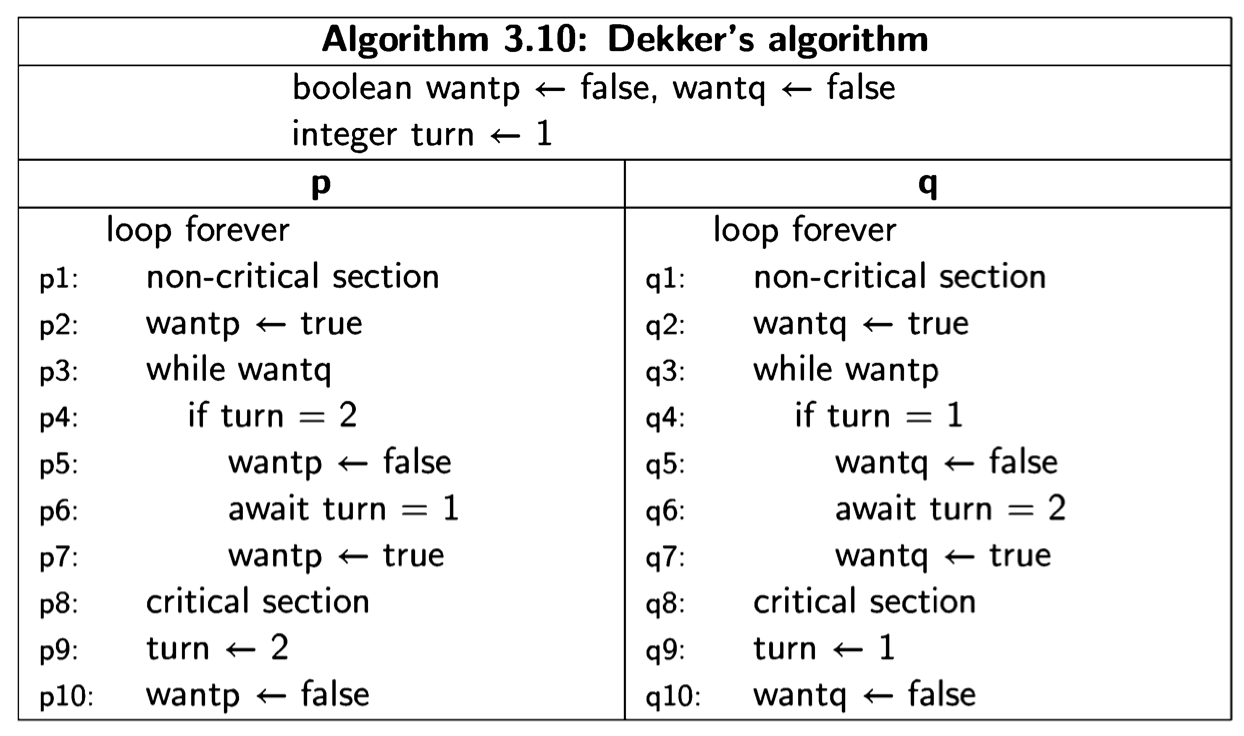
Recall that in the first attempt we explicitly passed the right to enter the critical section between the processes. Unfortunately, this caused the processes to be too closely coupled and prevented correct behavior in the absence of contention. In the fourth attempt, each process had its own variable which prevented problems in the absence of contention, but in the presence of contention both processes insist on entering their critical sections.

Dekker’s algorithm is like the fourth attempted solution, except that the right to insist on entering, rather than the right to enter, is explicitly passed between the processes. The individual variables wantp and wantq ensure mutual exclusion.

Suppose now that process p detects contention by finding wantq to be true at state- ment p3: while wantq. Process p will now consult the global variable turn to see if it is its turn to insist upon entering its critical section (\(turn \neq 2\), that is, \(turn = 1\)). If so, it executes the loop at p3 and p4 until process q resets wantq to false, either by terminating its critical section at q10 or by deferring in q5. If not, process p will reset wantp to false and defer to process q, waiting until that process changes the value of turn after executing its critical section.

Dekker’s algorithm is correct: it satisfies the mutual exclusion property and it is free from deadlock and starvation. The correctness properties by can be proved by constructing and analyzing a state diagram, but instead we will give a deductive proof in Section 4.5.