Proving correctness with state diagrams

States

You do not need to know the history of the execution of an algorithm in order to predict the result of the next step to be executed. Let us first examine this claim for sequential algorithms and then consider how it has to be modified for concurrent algorithms. Consider the following algorithm:

Suppose now that the computation has reached statement p2, and the values of a and b are 10 and 20, respectively. You can now predict with absolute certainty that as a result of the execution of statement p2, the value of a will become 150, while the value of b will remain 20; furthermore, the control pointer of the computer will now contain p3. The history of the computation how exactly it got to statement p2 with those values of the variables is irrelevant.

For a concurrent algorithm, the situation is similar:

Suppose that the execution has reached the point where the first process has reached statement p2 and the second has reached q2, and the values of a and b are again 10 and 20, respectively. Because of the interleaving, we cannot predict whether the next statement to be executed will come from process p or from process q; but we can predict that it will be from either one or the other, and we can specify what the outcome will be in either case.

In the sequential Algorithm 3.3, states are triples such as \(s_i = (p2, 10,20)\). From the semantics of assignment statements, we can predict that executing the statement p2 in state \(s_i\) will cause the state of the computation to change to \(s_{i+1} = (p3, 150, 20)\). Thus, given the initial state of the computation \(s_0 = (p1, 1, 2)\), we can predict the result of the computation. (If there are input statements, the values placed into the input variables are also part of the state.) It is precisely this property that makes debugging practical: if you find an error, you can set a breakpoint and restart a computation in the same initial state, confident that the state of the computation at the breakpoint is the same as it was in the erroneous computation.

In the concurrent Algorithm 3.4, states are quadruples such as \(s*i = (p2, q2, 10, 20)\). We cannot predict what the next state will be, but we can be sure that it is either \(s^{p}_{i+1} = (p3, q2, 150, 20) \) or \(s^{q}_{i+1} = (p2, q3, 10, 150) \) depending on whether the next state taken is from process p or process q, respectively. While we cannot predict which states will appear in any particular execution of a concurrent algorithm, the set of reachable states (Definition 2.5) are the only states that can appear in any computation. In the example, starting from state s;, the next state will be an element of the set \(\{s^{p}_{i+1},s^{q}_{i+1}\}\). From each of these states, there are possibly two new states that can be reached, and so on. To check correctness properties, it is only necessary to examine the set of reachable states and the transitions among them; these are represented in the state diagram.

For the first attempt, Algorithm 3.2, states are triples of the form \((p_i,q_j, turn)\), where turn denotes the value of the variable turn. Remember that we are assuming that any variables used in the critical and non-critical sections are distinct from the variables used in the protocols and so cannot affect the correctness of the solution. Therefore, we leave them out of the description of the state. The mutual exclusion correctness property holds if the set of all accessible states does not contain a state of the form (p3, q3, turn) for some value of turn, because p3 and q3 are the labels of the critical sections.

State diagrams

How many states can there be in a state diagram? Suppose that the algorithm has N processes with \(n_i\) statements in process i, and M variables where variable j has \(m_j\) possible values. The number of possible states is the number of tuples that can be formed from these values, and we can choose each element of the tuple independently, so the total number of states is \(n_1\ x \dots x\ n_N x\ m_1\dots x\ m_M\). For the first attempt, the number of states is \(n_1\ x\ n_2\ x\ m_1 = 4\ x\ 4\ x\ 2 = 32\), since it is clear from the text of the algorithm that the variable turn can only have two values, 1 and 2. In general, variables may have as many values as their representation can hold, for example, \(2^{32}\) for a 32-bit integer variable.

However, it is possible that not all states can actually occur, that is, it is possible that some states do not appear in any scenario starting from the initial state \(s_0 = (p1, q1, 1)\). In fact, we hope so! We hope that the states \((p3, q3, 1)\) and \((p3, q3, 2)\), which violate the correctness requirement of mutual exclusion, are not accessible from the initial state.

To prove a property of a concurrent algorithm, we construct a state diagram and then analyze if the property holds in the diagram. The diagram is constructed in- crementally, starting with the initial state and considering what the potential next states are. If a potential next state has already been constructed, then we can con- nect to it, thus obtaining a finite presentation of an unbounded execution of the algorithm. By the nature of the incremental construction, turn will only have the values 1 and 2, because these are the only values that are ever assigned by the algorithm.

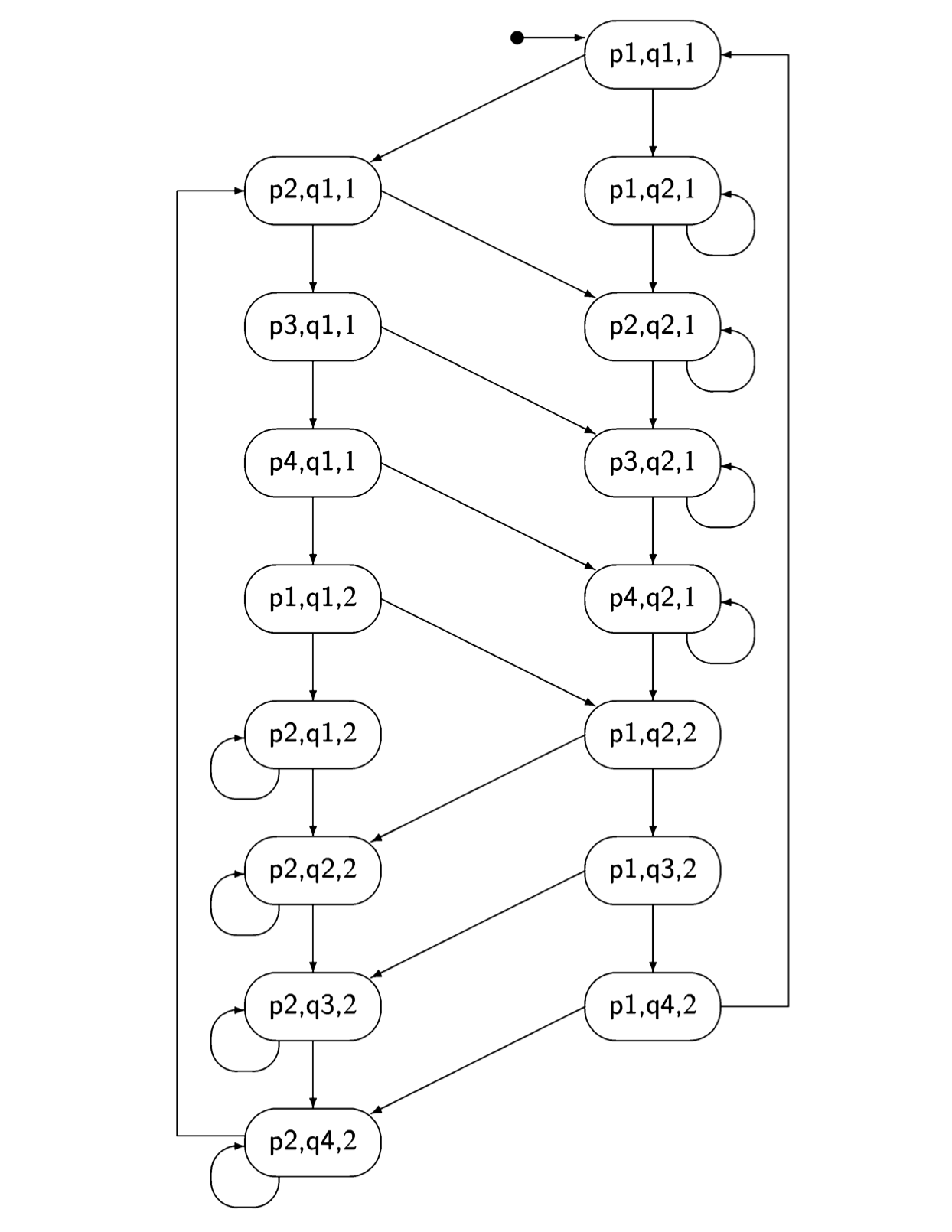
The following diagram shows the first four steps of the incremental construction of the state diagram for Algorithm 3.2:

The initial state is \((p1,q1, 1)\). If we execute pl from process p, the next state is \((p2,q1, 1)\): the first element of the tuple changes because we executed a statement of the first process, the second element does not change because we did not execute a statement of that process, and the third element does not change since by assumption the non critical section does not change the value of the variable turn. If, however, we execute ql from process q, the next state is \((p1, q2, 1)\). From this state, if we try to execute another statement, q2, from process q, we remain in the same state. The statement is await turn=2, but turn = 1. We do not draw another instance of \((p1, q2, 1)\); instead, the arrow representing the transition points to the existing state.

The incremental construction terminates after 16 of the 32 possible states have been constructed, as shown in Figure 3.1. You may (or may not!) want to check if the construction has been carried out correctly.

A quick check shows that neither of the states \((p3, q3, 1)\) nor \((p3, q3, 2)\) occurs; thus we have proved that the mutual exclusion property holds for the first attempt.

Abbreviating the state diagram

Clearly, the state diagram of the simple algorithm in the first attempt is unwieldy. When state diagrams are built, it is important to minimize the number of states that must be constructed. In this case, we can reduce the number of accessible states from 16 to 4, by reducing the algorithm to the one shown below, where we have removed the two statements for the critical and non-critical sections.

Admittedly, this is suspicious. The whole point of the algorithm is to ensure that mutual exclusion holds during the execution of the critical sections, so how can we simply erase these statements? The answer is that whatever statements are executed by the critical section are totally irrelevant to the correctness of the synchronization algorithm.

If in the first attempt, we replace the statement p3: critical section by the com- ment p3: // critical section, the specification of the correctness properties remain unchanged, for example, we must show that we cannot be in either of the states \((p3, q3, 1)\) or \((p3, q3,2)\). But if we are at p3 and that is a comment, it is just as if we were at p4, so we can remove the comment; similar reasoning holds for p1. In the abbreviated first attempt, the critical sections have been swallowed up by \(turn \leftarrow 2\) and \(turn \leftarrow 1\), and the non-critical sections have been swallowed up by await \(turn=1\) and await \(turn=2\). The state diagram for this algorithm is shown in Figure 3.2, where for clarity we have given the actual statements and variables names instead of just labels.