A monitor solution for the dining philosophers

Algorithm 6.10, an attempt at solving the problem of the dining philosophers with semaphores, suffered from deadlock because there is no way to test the value of two fork semaphores simultaneously. With monitors, the test can be encapsulated, so that a philosopher waits until both forks are free before taking them.

Algorithm 7.5 is a solution using a monitor. The monitor maintains an array fork which counts the number of free forks available to each philosopher. The takeForks operation waits on a condition variable until two forks are available. Before leaving the monitor with these two forks, it decrements the number of forks available to its neighbors. After eating, a philosopher calls releaseForks, which, in addition to updating the array fork, checks if freeing these forks makes it possible to signal a neighbor.

Let eating[i] be true if philosopher i is eating, that is, if she has successfully executed takeForks(i)and has not yet executed releaseForks(i). We leave it as an exercise to show that \(eating[i] \leftrightarrow (forks[i] = 2)\) is invariant. This formula expresses the requirement that a philosopher eats only if she has two forks.

Theorem 7.5 Algorithm 7.5 is free from deadlock.

Proof: Let E be the number of philosophers who are eating, In the exercises, we ask you to show that the following formulas are invariant:

\[\neg empty(OKtoEat[i]) \rightarrow (fork[i] < 2)\ \ \ \ (7.1)\] \[\sum_{i=0}^{4} fork[i] = 10 - 2 * E\ \ \ \ (7.2)\]

Deadlock implies E = 0 and all philosophers are enqueued on OKtoEat. If no philosophers are eating, from (7.2) we conclude \(\sum fork[i] = 10\). If they are all enqueued waiting to eat, from (7.1) we conclude \(\sum fork[i] \leq 5\) which contradicts the previous formula.

Starvation is possible in Algorithm 7.5. Two philosophers can conspire to starve their mutual neighbor as shown in the following scenario (with the obvious abbreviations):

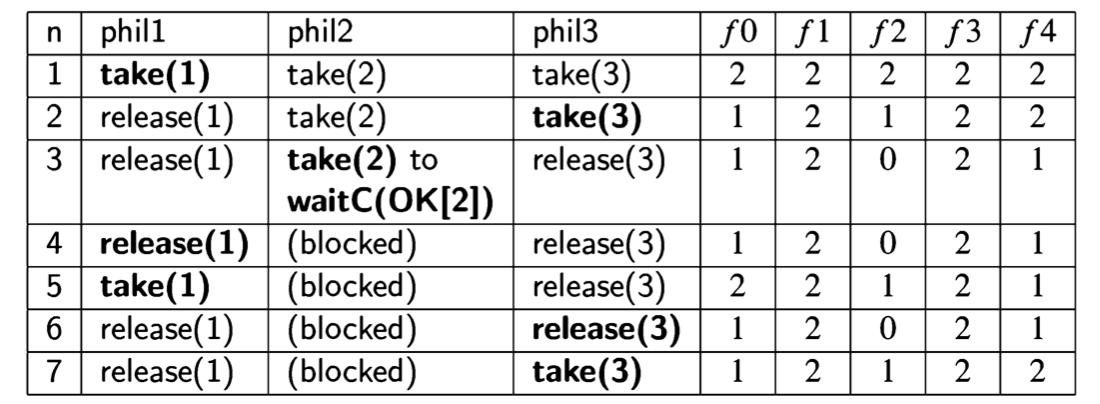
Philosophers 1 and 3 both need a fork shared with philosopher 2. In lines 1 and 2, they each take a pair of forks, so philosopher 2 is blocked when trying to take forks in line 3. In lines 4 and 5 philosopher 1 releases her forks and then immediately takes them again; since forks[2] does not receive the value 2, philosopher 2 is not signaled. Similarly, in lines 6 and 7, philosopher 3 releases her forks and then immediately takes them again. Lines 4 through 7 of the scenario can be continued indefinitely, demonstrating starvation of philosopher 2.