Fourth attempt

In the third attempt, when a process sets the variable want to true, not only does it indicate its intention to enter its critical section, but also insists on its right to do so. Deadlock occurs when both processes simultaneously insist on entering their critical sections. The fourth attempt to solve the critical section problem tries to remedy this problem by requiring a process to give up its intention to enter its critical section if it discovers that it is contending with the other process (Algorithm 3.9). The assignment p4: \(wantp\leftarrow false\) followed immediately by an assignment to the same variable p5: \(wantp\leftarrow true\) would not be meaningful in a sequential algorithm, but

it can be useful in a concurrent algorithm. Since we allow arbitrary interleaving of statements from the two processes, the second process may execute an arbitrary number of statements between the two assignments to wantp. When process p relinquishes the attempt to enter the critical section by resetting wantp to false, process q may now execute the await statement and succeed in entering its critical section.

A State diagram or deductive proof will show that the mutual exclusion property is satisfied and that there is no deadlock. However, a scenario for starvation exists as shown by the cycle in Figure 3.5. The interleaving is “perfect” in the sense that the execution of a statement by process q is always followed immediately by the execution of the equivalently-numbered statement in process p. In this scenario, both processes are starved.

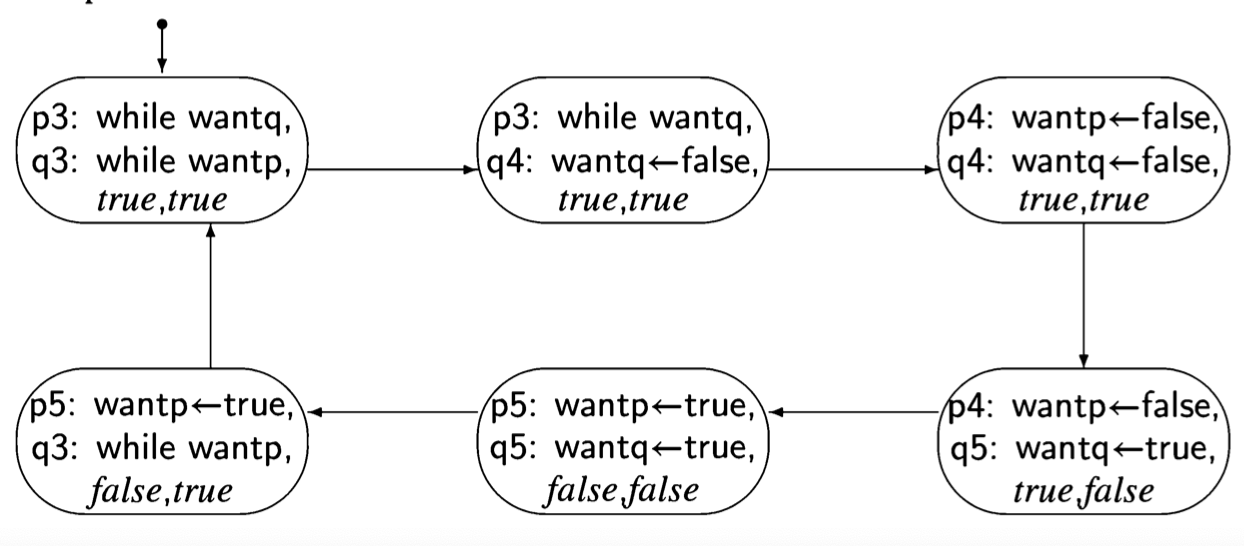
At this point, most people object that this is not a “realistic” scenario; we can hardly expect that whatever is causing the interleaving can indefinitely ensure that exactly two statements are executed by process q followed by exactly two statements from p. But our model of concurrency does not take probability into account. Unlikely scenarios have a nasty way of occurring precisely when a bug would have the most dangerous and costly effects. Therefore, we reject this solution, because it does not fully satisfy the correctness requirements.