The critical section problem for two processes

Using semaphores, the solution of the critical section problem for two processes is trivial (Algorithm 6.1). A process, say p, that wishes to enter its critical section executes a preprotocol that consists only of the wait(S) statement. If S.V = 1 then S.V is decremented and p enters its critical section. When p exits its critical section and executes the postprotocol consisting only of the signal(S) statement, the value of S.V will once more be set to 1.

If q attempts to enter its critical section by executing wait(S) before p has left, S.V = 0 and q will become blocked on S. S, the value of the semaphore S, will become (0, {q}). When p leaves the critical section and executes signal(S), the arbitrary process in the set S.L = {q} will be q, so that process will be unblocked and can continue into its critical section.

The solution is similar to Algorithm 3.6, the second attempt, except that the definition of the semaphore operations as atomic statements prevents interleaving between the test of S.V and the assignment to S.V.

To prove the correctness of the solution, consider the abbreviated algorithm where the non-critical section and critical section statements have been absorbed into the following wait(S) and signal(S) statements, respectively.

The state diagram for this algorithm is shown in Figure 6.1. Look at the state in the top center, which is reached if initially process p executes its wait statement, successfully entering the critical section. If process q now executes its wait statement, it finds S.V = 0, so the process is added to S.L as shown in the top right state. Since q is blocked, there is no outgoing arrow for q, and we have labeled the only arrow by p to emphasize that fact. Similarly, in the bottom right state, p is blocked and only process q has an outgoing arrow.

A violation of the mutual exclusion requirement would be a state of the form (p2: signal(S), q2: signal(S), ...). We immediately see that no such state exists, so we conclude that the solution satisfies this requirement. Similarly, there is no deadlock, since there are no states in which both processes are blocked. Finally,

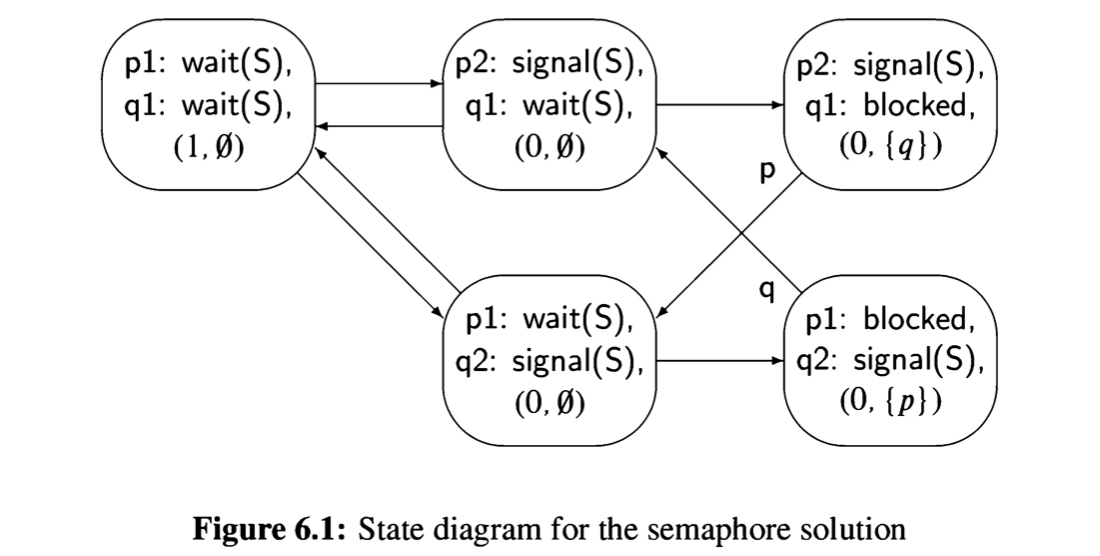
the algorithm is free from starvation, since if a process executes its wait statement (thus leaving the non-critical section), it enters either the state with the signal statement (and the critical section) or it enters a state in which it is blocked. But the only way out of a blocked state is into a state in which the blocked process continues with its signal statement.